-
В правильном треугольнике ABC со стороной AB = 4 см, через вершину A проведено перпендикуляр АМ к плоскости треугольника ABC, AM = 4√3 см.
А) Докажите, что прямая BC перпендикулярна
плоскости AMP, где P - середина стороны BC.
Б) Найдите расстояние от точки M до прямой BC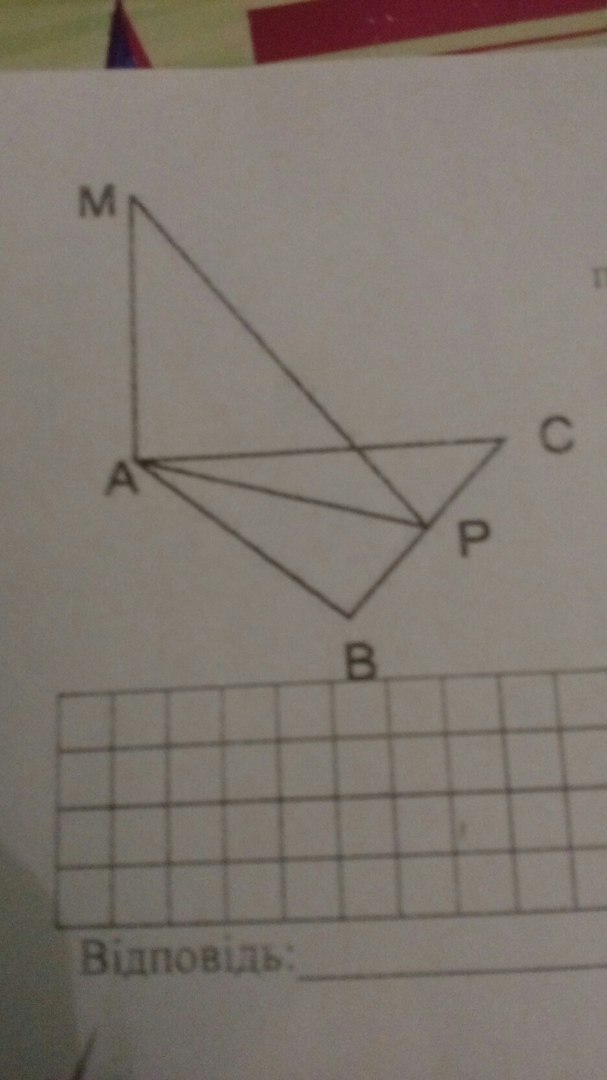
-
Предмет:
Геометрия -
Автор:
rupertostevenson - 6 лет назад
-
Ответы 1
-
ABC - равносторонний, где AP - высота, медиана, биссектриса. ⇒ AP ⊥ BC. Плоскость перпендикулярна, если прямая, лежащая в плости, перпендикулярна, а раз AP ⊥ BC, то плоскость AMP ⊥ BCВысота в равностороннем треугольнике -
a = 4. Высота, AP, равна 2√3. Рассмотрим треугольник MAP, MA ⊥ AP - треугольник прямоугольный. MP² = MA² + AP² по теореме ПифагораMP² = 60. MP = 4√15
-
Автор:
saigeacevedo - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
как появились все голактики
-
Предмет:
Биология -
Автор:
sebastianulzc - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
1. Школа, вересень, друзі, п’ять. 2. Зустрітися, зрадіти, весело, навчатися. 3. В, і, до, за. 4. Привітний, зелень, світлий, урочистий. 5. Він, п’ятнадцять, шістнадцять, дев’ять. 6. Радо, доброзичливий, уважно, сьогодні. 7. А, і, Срочно
-
Предмет:
Українська мова -
Автор:
snuggles - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
почему творчество влияло на развитие труда
-
Предмет:
Обществознание -
Автор:
carlasingleton - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
как звали ученика Н.Н.Зинина
-
Предмет:
Другие предметы -
Автор:
camryn8xg1 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
