Задать вопрос Регистрация
Помочь другим

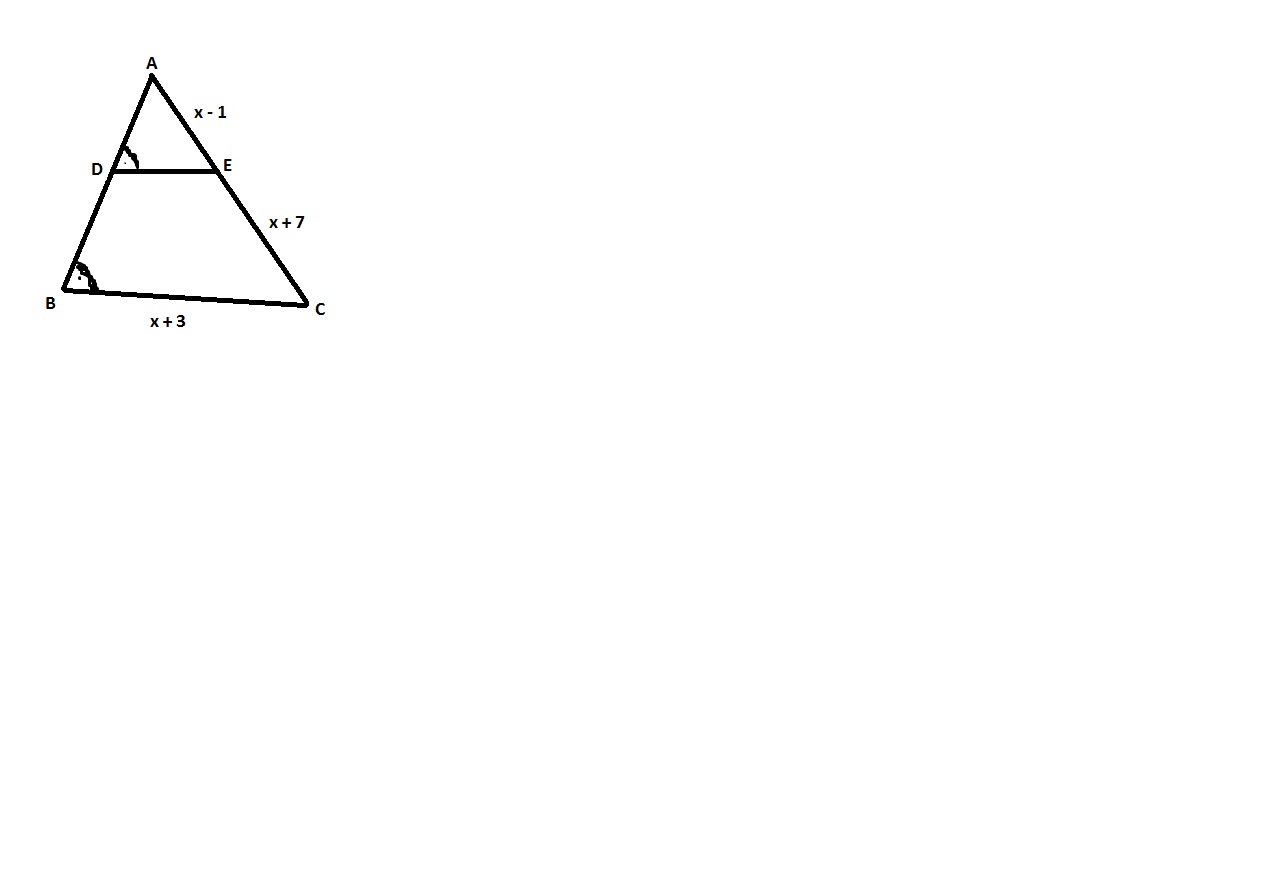
  • Если <ABC ~ <ADE, |DE| = 1, |AE| = x - 1, |EC| = x + 7 и |BC| = х + 3, то найдите длину стороны |AC|. Рисунок во вложении.

    question img

Ответы 2

  • х + 3 = (2х + 6)/(х - 1)(х + 3) (х - 1) - 2х + 6 = 0 х² + 2х - 3 - 2х + 6 = 0х² - 9 = 0х = 3.2х + 6 = 12.Ответ:  lАСl = 12

  • Поскольку ΔABC~ΔADE по первому признаку подобия треугольников, то:

    \frac{x+3}{1}=\frac{(x-1)+(x+7)}{x-1}\\\\(x+3)(x-1)=2x+6\\\\x^2-x+3x-3=2x+6\\\\x^2=9\\\\x=3\\\\AC=(x-1)+(x+7)=3-1+3+7=12

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years