-
На рисунке отрезок МК параллелен стороне АС. Луч МN является биссектрисой угла ВМК. Найдите величину угла MNK.
Заранее спасибо!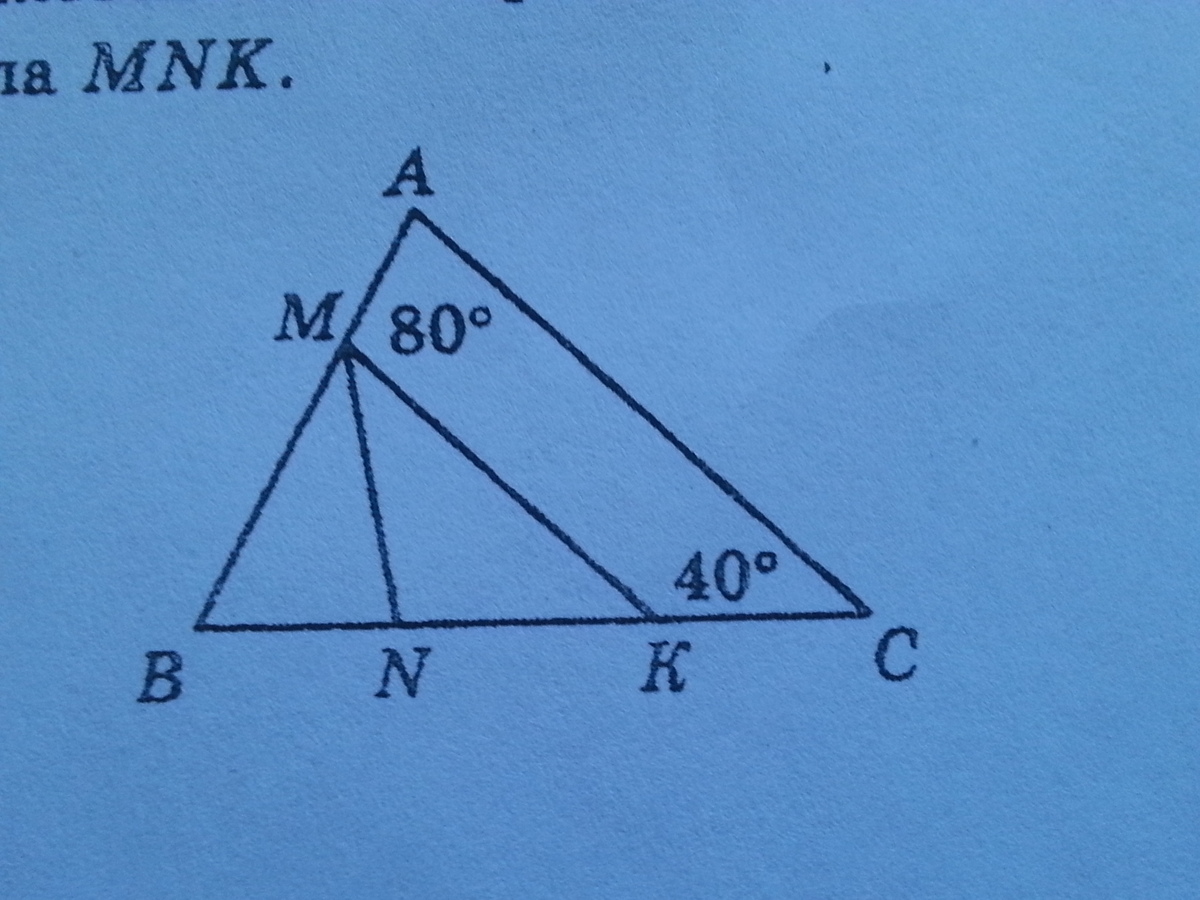
Ответы 1
-
Решение:
1) Рассмотрим треугольник АВС
По теореме о сумме углов треугольника найдем угол В.
Угол В = 180° - угол А - угол С = 180° - 80° - 40° = 60°
2) Угол ВМK = углу А (соответственные при МК || АС и секущей АВ)
Угол ВМK = 80°
3) Угол ВМN = углу MKN (т.к. MN - биссектриса угла ВМК)
Угол ВМN = углу MKN = 80° : 2 = 40°
4) Рассмотрим треугольник ВМN
По теореме о сумме углов треугольника найдем угол МNВ.
Угол MNB = 180° - угол В - угол ВМN = 180° - 60° - 40° = 80°
5) Сумма углов MNB и MNK равна 180°, т.к. они смешные.
Отсюда угол MNK = 180° - угол MNB = 180° - 80° = 100°
Ответ: угол MNK = 100°
-
Автор:
baron - 5 лет назад
-
0
-
-
Добавить свой ответ
-
у буратино было 20 сольдо из которых40% он потратил на азбуку сколько сольдо буратино потратил на азбуку
-
Предмет:
Математика -
Автор:
onyxsellers - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Чехов лошадиная фамилия за счет чего создается комический эффект рассказа. помогите пожалуйста очень срочно надо. в. г. Распутин прочитать произведения уроки французского смысл название рассказа.
-
Предмет:
Литература -
Автор:
christinea0jk - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Из 76 м ткани сшили 8 одиннаковых платьев и 13 халатов.На одно платье расходовали 3 м ткани.Сколько метров ткани расходовали на один халат?
-
Предмет:
Математика -
Автор:
raveniwbg - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
на обычных весах в магазине , самое мелкое деление которых соответствует 10г
продавец отвесил 800г конфет и 550г крупы , сравните качество измерения массы конфет и крупы оценив относительные погрешности в процентах
