АВСДА1В1С1Д1 - правильная призма. Точка М делит сторону А1С1 на равные части. СС1 = 4 . А1С1 = 6. Найдите периметр сечения призмы плоскостью ВМС. Я решила, но с ответом не сходится. Помогите пожалуйста. ))))))))))))))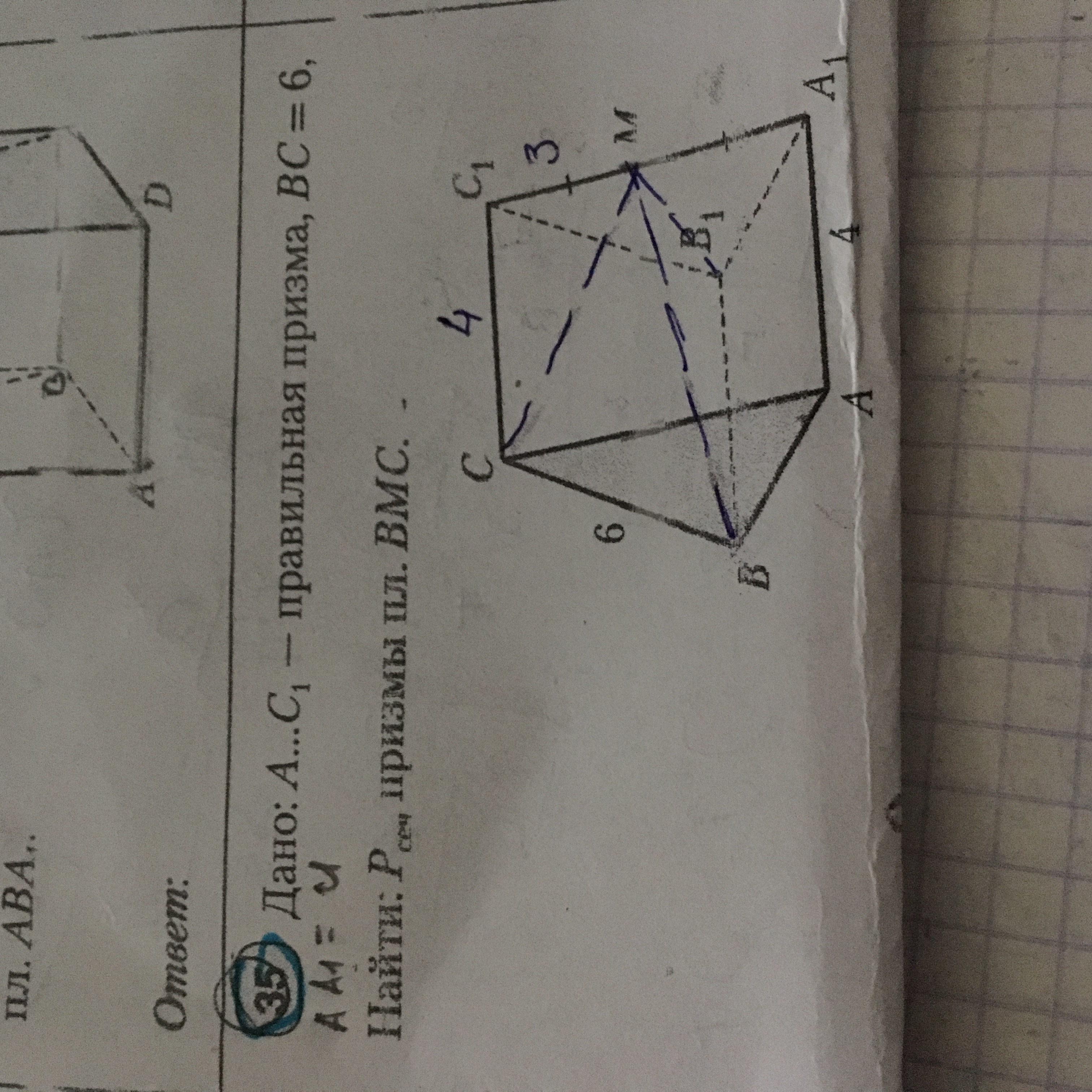

Ответы 2

ответ не верный. Я вчера решила сама.
- Автор:
  snuggles34
- 5 лет назад
- 0
АВСДА1В1С1Д1 - правильная призма. Точка М делит сторону А1С1 на равные части. СС1 = 4 . А1С1 = 6. Найдите периметр сечения призмы плоскостью ВМС. Решение: Плоскость ВМС отсекает в правильной призме равнобедренную усеченную трапецию BMKC. Причем точка находится на середине ребра В1А1. Длина отрезка МК(верхнее основание трапеции) как средней линии треугольника А1В1С1 равна половине длины В1С1 МК =В1С1/2 =6/2=3Дина нижнего основания трапеции равна ВС=6Боковые стороны CМ и BК равны и найходятся по тереме Пифагора из треугольника СС1М $CM = \sqrt{CC_1^2+C_1M^2} = \sqrt{4^2+3^2}=5$ Определим высоту трапеции $h = \sqrt{CM^2-( \frac{BC-MK}{2} )^2}= \sqrt{5^2- (\frac{6-3}{2})^2 } = \frac{9}{2}=4,5$ Находим площадь трапеции по формуле $S = \frac{MK+CB}{2}*h= \frac{6+3}{2}* \frac{9}{2}= \frac{81}{4}= 20,25$
- Автор:
  matildagqnn
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы