-
Помогите пожалуйста, не сильна в геометрии(
Решите, сколько сможете, буду благодарна!
(Если вы случайно знаете, из какой книги распечатаны эти задания, просьба написать)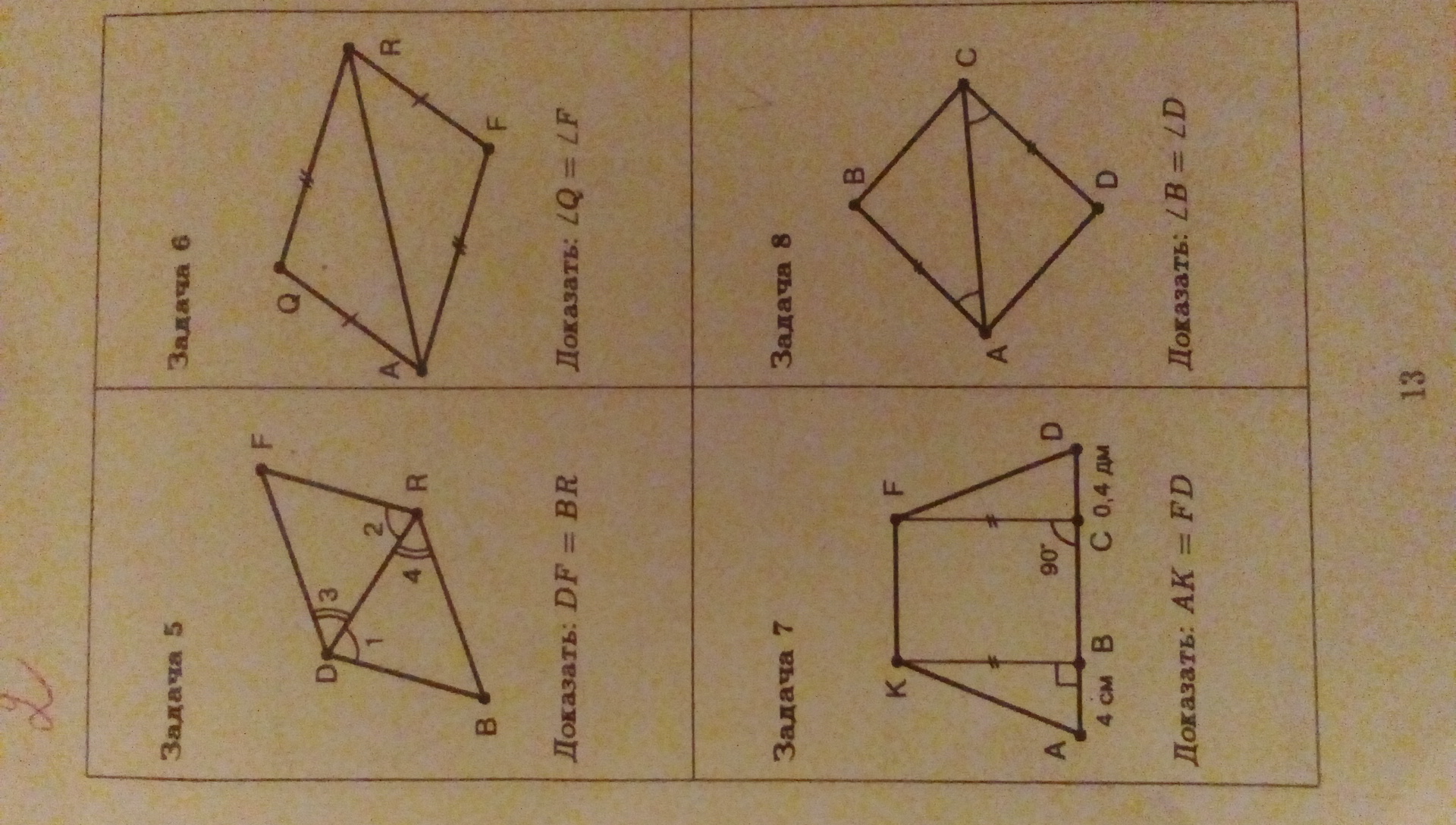
Ответы 2
-
Огромное спасибо!!!
-
Автор:
remingtonwhitehead - 6 лет назад
-
0
-
-
5. Рассмотрим DFBR:1)угол 1 = углу 2 (накрест лежащие при прямых BD и FR и секущей DR)2) угол 3 = углу 4 (накрест лежащие при прямых DF и BR и секущей DR) => DFBR - параллелограм => DF||BR => DF=BR что требовалось доказать.6. Рассмотрим ∆AQR и ∆ARF:1) AQ=FR (по условию задачи)2) QR=AF (по условию задачи)3) AR - общая=> ∆AQR=∆ARF по 3 признаку равенства треугольников => угол Q = углу F что требовалось доказать.7. Рассмотрим ∆AKB и ∆CFD:1) KB=FC (по условию задачи)2) AB=CD (т.к. о,4дм=4см, 4см=4см)3) угол B = углу С (т.к. 180°-90°= углу FCD(по правилу смежных углов) 90°=90°)=> ∆AKB=∆CFD по 1 признаку равенства треугольников => AK=FD что требовалось доказать.8. Рассмотрим ∆ABC и ∆ACD1) AB=CD (по условию задачи)2) угол BAC = углу ACD (по условию задачи)3) AC - общая=> ∆ABC=∆ACD по 1 признаку равенства треугольников => угол B = углу D что требовалось доказать.
-
Автор:
einstein48 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
СРОООООЧНОООО!!!!!Поезд пробыл в пути 25 часов, средняя скорость поезда 72 км/час. Сколько километров пути прошел поезд, если общее время стоянки поезда составляет 6 часов?
-
Предмет:
Математика -
Автор:
tasha41 - 6 лет назад
-
Ответов:
7 -
Смотреть
-
-
Літературне читання 3клас стр.57 по малюнку скласти текст-розповідь. Прийшла золота осінь. Татусь взяв Михайлика та Татьянку в ліс по гриби. Помогите продолжить текст пожалуйста!
-
Предмет:
Українська література -
Автор:
adánzudw - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
растворимые и не растворимые в воде вещества
-
Предмет:
Окружающий мир -
Автор:
beau - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
2. Jess is ........ (tall) Ellie. 3. Mina is..... (happy) girl. 4. Ellie is.... (short) girl. 5. Jess has got ..... (short) hair. 6. Ellie has got ...... (long) hair than Jess. 7. Mina is....... (tall) girl. 8. Ellie has got (long) hair. 9. Mina is..... (tall) Jess.
-
Предмет:
Английский язык -
Автор:
felix4jzp - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
