геометрия, 8 класс
подробное решение задачи

да, объясни, если будет несложно

Средним геометрическим XY для двух чисел a и b является такое число, равное √ab. В прямоугольном треугольнике средним геометрическим для проекций (частей гипотенузы, разделенных высотой) яаляется высота, проведённая к этой гипотенузе. Доказать это можно, рассматривая подобие треугольников.

спасибо большое)

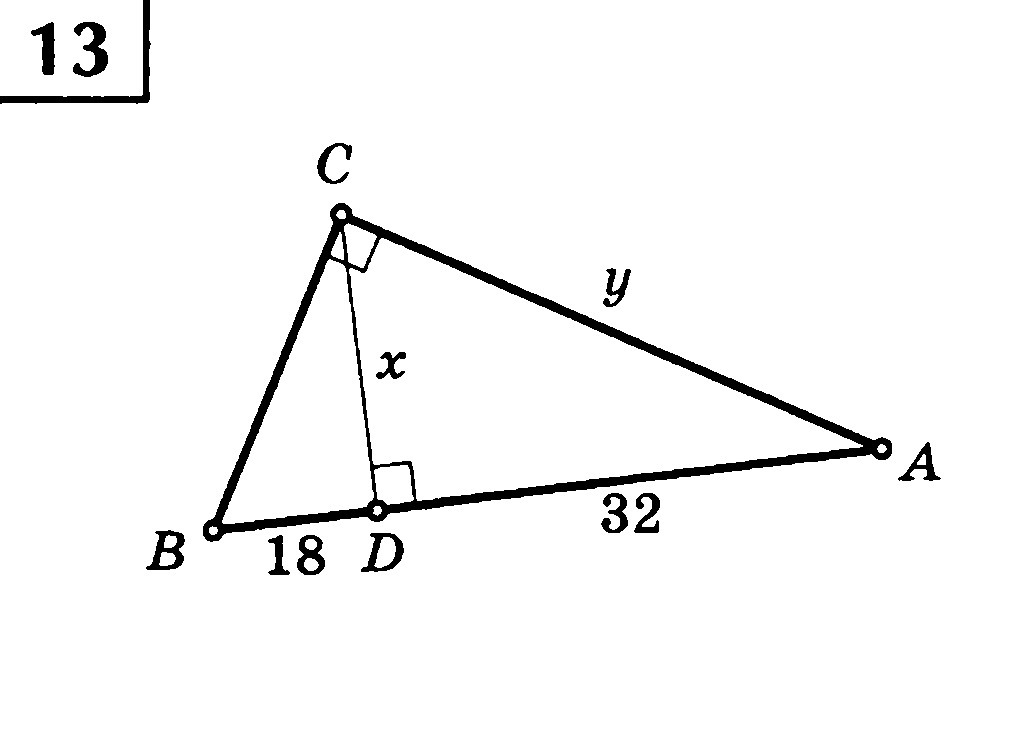
Треугольник является прямоугольным, кроме того, к гипотерузе проведена высота. В прямоугольном треугольнике высота, проведённая к гипотенузе, является средним геометрическим для проекций, т.е. х = √BD•DAx = √18•32 = √576 = 24y можно найти по теореме Пифагора:y = √x² + AD² = √24² + 32² = √576 + 1024 = √1600 = 40.Ответ: х = 24; у = 40.P.s.: если непонятно, что такое среднее геометрическое, то пиши, объясню.