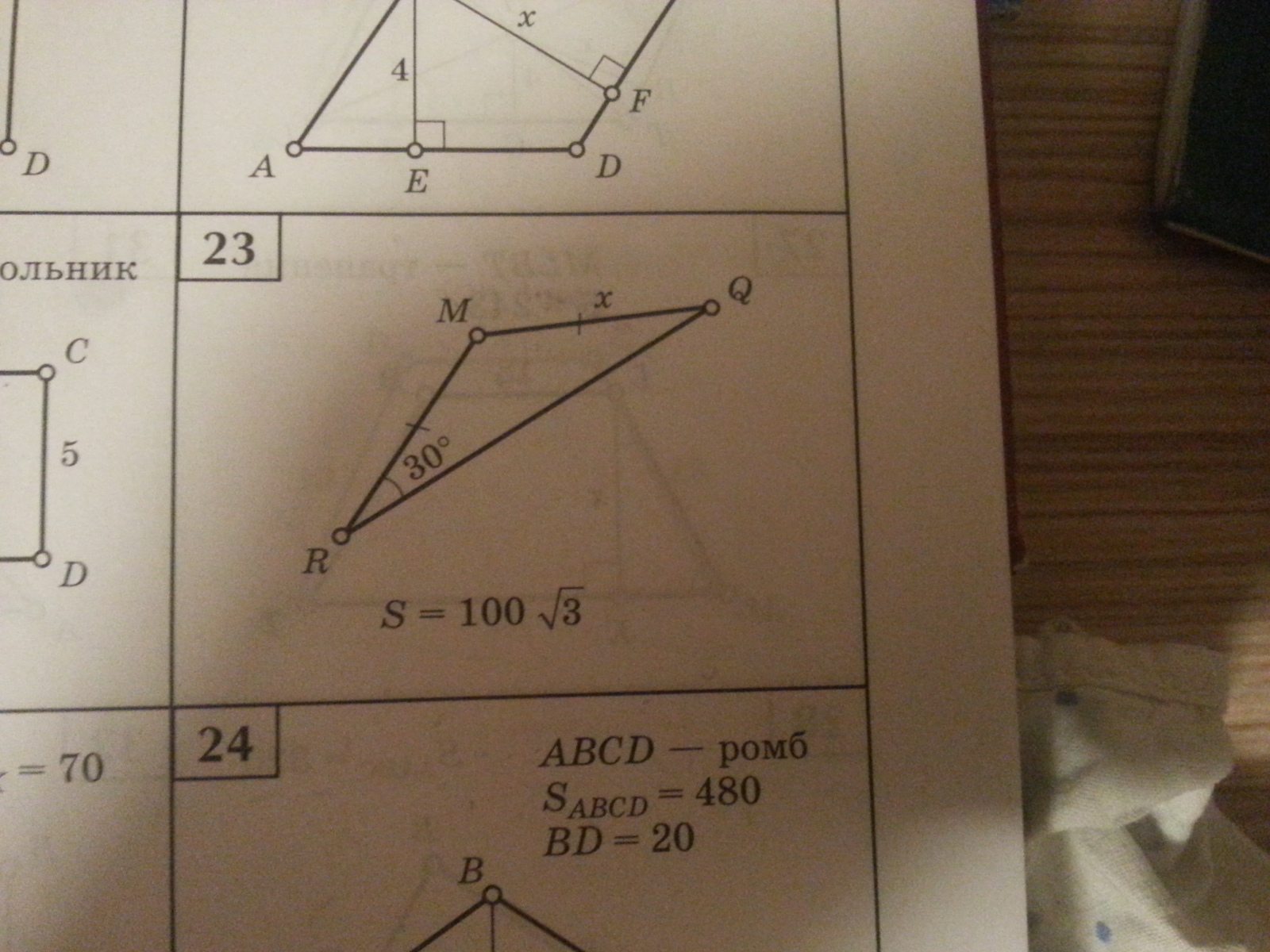
Помогите СРОЧНО!!! Решить по теореме пифагора, найти x. N 23

Решение по теореме Пифагора:Опустим высоту MH из вершины M на основание RQ.Треугольник RMQ равнобедренный (MR=RQ - дано), значитMH - высота и медиана.Медиана делит треугольник на два РАВНОВЕЛИКИХ треугольника.Значит Srmh=Srmq/2=50√3.Площадь треугольника RMH равна S=(1/2)*RH*MH. Отсюда MH*RH=100√3 (1).Треугольник RMH  прямоугольный с углом <MRH=30° (дано). Значит MR=2MH (так как катет MH лежит против угла 30 градусов).По Пифагору MR²=MH²+RH²  или MR²-MH²=RH² или3MH²=RH². RH=MH√3 (2).Подставим (2) в (1): МН*MH√3=100√3. ОтсюдаМН²=100. МН=10.Тогда MR=2*MH=20.