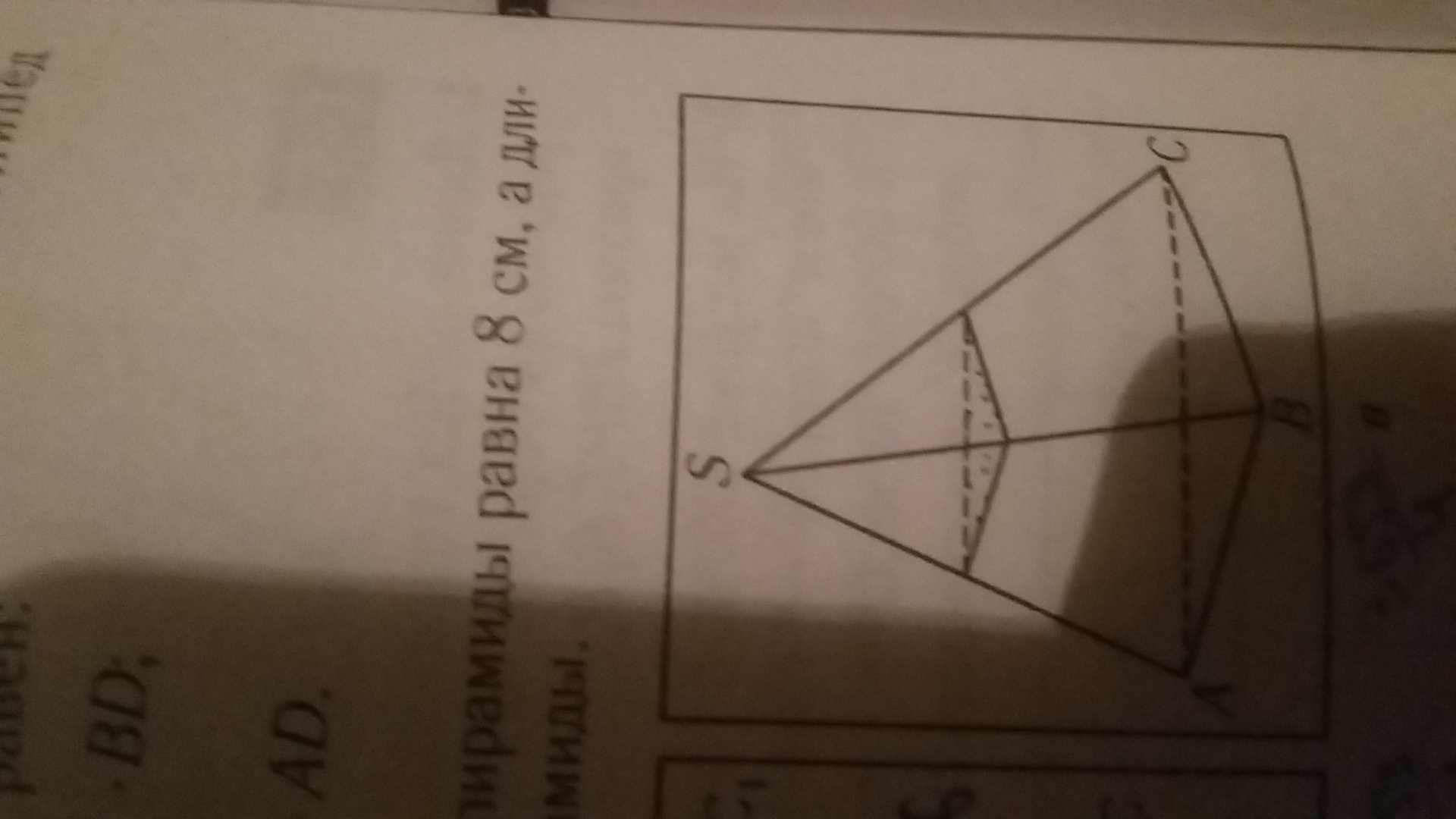
В треугольной пирамиде SABC сечение, параллельное грани АВС, делит ребро SA в отношении 3:4, считая от точки S. Вычислите расстояние от точки S пирамиды до плоскости АВС, если площадь сечения равна 90 см^2, а объем пирамиды равен 210 см^3.

V( пирамиды SABC)=(1/3)·S(ΔABC)·HПо условию (1/3)·S(ΔABC)·H=210, значит  S(ΔABC)·H=630.Пусть сечение - треугольник А₁В₁С₁.Из подобия  Так как SA₁:SA=3:7 , то  h:H=3:7, где  h- высота пирамиды SA₁B₁C₁иА₁В₁:АВ=3:7В₁С₁:ВС=3:7А₁С₁:АС=3:7а площади подобных треугольников относятся как квадраты соответствующих сторон.S( Δ А₁В₁С₁):S( Δ АВС)=9:49Так какS(Δ А₁В₁С₁)=90, то S(Δ АВС)=90·49:9=490Из равенства S(ΔABC)·H=630  находим Н=630:490Н=9/7h:H=3:7h=27/49О т в е т. 27/49.