-
Помогите плиз, ничего в геометрии не понимаю:
На рисунке 113 изображен квадрат ABCD, стороны которого продолжены так, что AP = BQ = CR = DS. Докажите что четырехугольник PQRS - квадрат.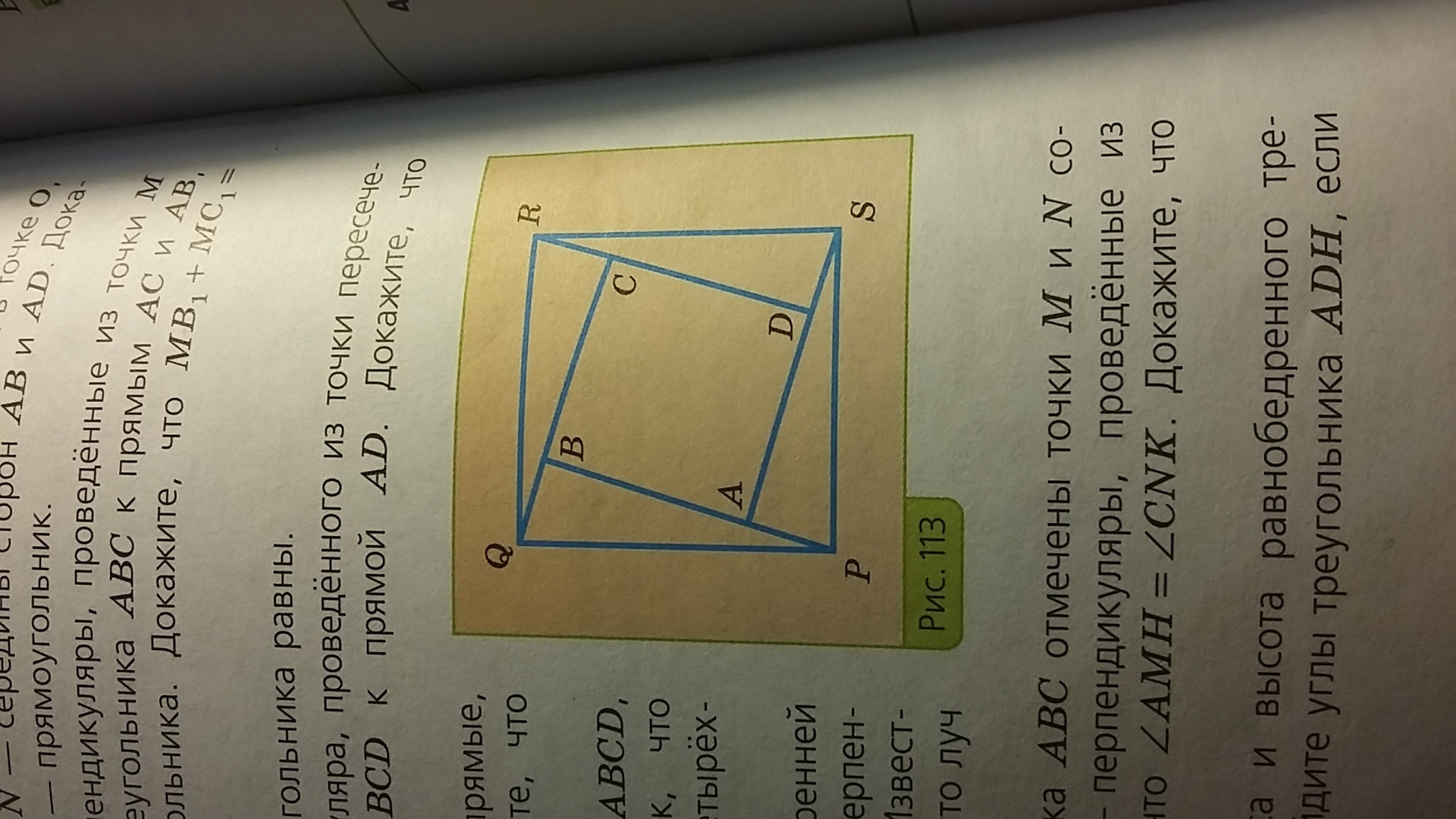
Ответы 1
-
Рассмотрим ∆PQB и ∆QRC.QB = PAPB = QC (т.к. BC = AB и QC = QB + BC, PB = PA + AB).∠QCR = 90° - как смежный угол с прямым углом.Аналогично ∠ABQ = 90°.Тогда ∆PQB = ∆QRC - по двум катетам.Из равенства треугольников => QR = AQ, ∠QPB = ∠RQC и ∠PQB = ∠QRC.Аналогично ∆PAS = ∆SDR (AS = DR, AP = CR, ∠PAS = ∠RDS = 90°). Из этого равенства следует, что PS = RS.Рассмотрим ∆PQB и ∆SAP.Они также равны ( AS = PB, AP = QB, ∠PAS = ∠PBQ = 90°).Из всех равенства следует, что QR = RS = PS = QP. Тогда QRSP - ромб. Но ∠PQB + ∠CQR = 90° - ∠QPB + ∠CQR = 90° - ∠QPB + ∠QPB => QRSP - квадрат (его стороны равны и перпендикулярны друг другу).
-
Автор:
carla - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
на соревнованиях спортсмен пробежал дистанцию длиной 700 метров за одну минуту 40 секунд С какой скоростью спортсмен пробежит дистанцию
-
Предмет:
Математика -
Автор:
atkins - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
1) 7 - 5 1/4
2) 6 - 5 2/3
3) 12-9 3/8
4) 11-6 2/3
5) 8-3 2/7
6) 5 6/13-2
7) 9 3/10 -4
8) 2 3/14- 1-
Предмет:
Математика -
Автор:
ferrisrobbins - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
На стройплощадку нужно перевезти груз, состоящий из бетонных плит массой по 300 кг, балок массой по 48 кг и кирпичей массой по 3 кг. Какова наибольшая возможная масса груза (в килограммах), если весь груз можно перевезти на грузовике грузоподъёмностью 5 т?
ПОДРОБНО ОБЪЯСНИТЕ КАК РЕШАТЬ -
написать на листочках сочинение-описание. описать один из трудовых процессов (как помыть посуду, убрать в комнате, работать на даче и тд) ПЖ ПОМОГИТЕ!!!
-
Предмет:
Русский язык -
Автор:
nicolas91 - 5 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
