-
С помощью теоремы синусов, теоремы косинусов и таблицы Брадиса решите треугольник ABC.
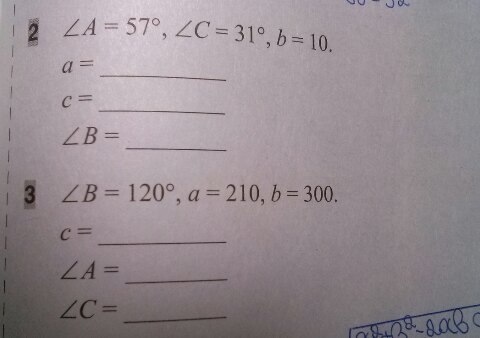
Ответы 1
-
2) ∠B=180-∠A-∠C=180-57-31=92°Согласно теореме синусов
(где А, В, C - соответствующие углы)
3) По теореме синусов найдем ∠А
⇒ ∠A≈37,5°∠C=180-∠B-∠C=180-120-37,5=22,5°По теореме косинусов найдем сc²=a²+b²-2ab*CosC=210²+300²-2*210*300*0,92=18180 ⇒ c≈135
-
Автор:
aliceumyy - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Cколько часов пройдёт с 18 часов 28-го марта до 10 часов 2-го апреля ?
-
Предмет:
Математика -
Автор:
saramcgee - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
найди значение выражения 10 10/11÷12/2 21/22×6 1/2
-
Предмет:
Математика -
Автор:
leopoldo - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Написать present perfect или past simple. Очень надо, пожалуйста
-
Предмет:
Английский язык -
Автор:
adams - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
запиши похожую пословицу как Люби кататься люби и саночки возить
-
Предмет:
Литература -
Автор:
vidal22 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
