С помощью теоремы синусов, теоремы косинусов и таблицы Брадиса решите треугольник ABC.

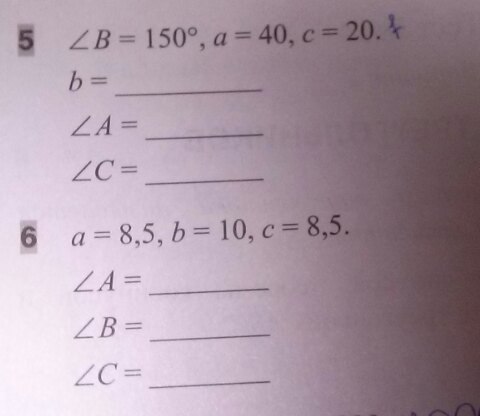
Ответы 1

5) По теореме косинусов найдем значение b (полагая что ∠B лежит напротив стороны b)b²=a²+c²-2ac*Cos∠B=40²+20²-2*40*20*Cos(150°)⇒b≈58 условных единиц длиныНедостающие углы найдем по теореме синусов $\frac{a}{SinA}= \frac{b}{SinB}= \frac{c}{SinC}$ (под SinA подразумевается Sin∠A и т.д.) $SinA= \frac{a*SinB}{b}= \frac{40*Sin150}{58}$ ≈0,34 ⇒ ∠A≈20° $SinC= \frac{c*SinB}{b}= \frac{20*Sin150}{58}$ ≈0,17⇒ ∠C≈10°(можно сделать проверку - сложив все углы и убедиться что их сумма равна 180°)6) По теореме косинусов найдем все углы $CosA= \frac{b^{2}+c^{2}-a^{2}}{2bc}= \frac{10^{2}+8,5^{2}-8,5^{2}}{2*8,5*10}$ ≈0,59 ⇒ ∠A≈54°Так как длина сторон а и с равна, то соответственно противоположные им углы - равны, т.е. ∠A=∠С≈54°(можно пересчитать по схожей схеме, числа будут те же) $CosB= \frac{a^{2}+c^{2}-b^{2}}{2ac}= \frac{8,5^{2}+8,5^{2}-10^{2}}{2*8,5*8,5}$ ≈0,31 ⇒ ∠B≈72°Сложив все углы получаем итоговую сумму 180°, значит расчеты выполнены верно
- Автор:
  basileowood
- 5 лет назад
- 0
Добавить свой ответ