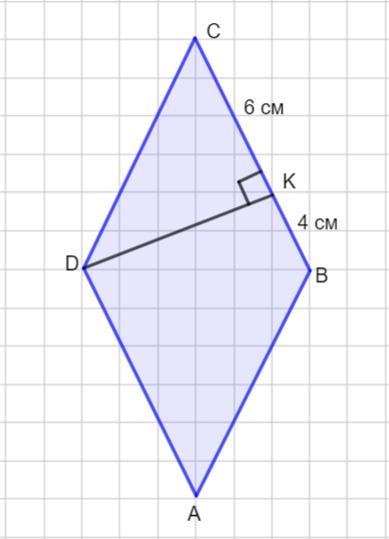
В ромбе ABCD из вершины тупого угла D к стороне BC проведена перпендикуляр DK.BK=4 см,KC=6см.Вычислите площадь ромба ABCD (в см^2) ПОМОГИТЕ СРОЧНО ПОЖАЙЛУСТА

Ответ:

Площадь ромба равна 80 см ².

Объяснение:

В ромбе АВСD из вершины тупого угла D к стороне ВС проведен перпендикуляр DK . ВК =4 см, КС = 6 см. Вычислить площадь ромба.

По условию из вершины тупого угла D к стороне  ВС проведен перпендикуляр DK. Значит, отрезок DK является высотой ромба.

Точка К делит сторону ВС на два отрезка ВК =4 см, КС = 6 см.

Тогда сторона ВС =ВК +КС ;

ВС =4 + 6 =10 см.

Ромб - это параллелограмм, у которого все стороны равны.

Значит, АВ =ВС =СD=АD = 10 см.

Рассмотрим ΔDКМ - прямоугольный. СD = 10 см, СК = 6см

Применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

И найдем катет DК

DC^{2} =DK^{2} +KC^{2} ;\\DK^{2} =DC^{2} -KC^{2};\\DK= \sqrt{DC^{2} -KC^{2}} ;\\DK= \sqrt{10^{2} -6^{2} } =\sqrt{100-36} =\sqrt{64} =8

Тогда высота ромба DК = 8см.

Найдем площадь ромба как произведение стороны ромба на высоту.

S = BC \cdot DK;\\S =10\cdot 8=80

Значит, площадь ромба равна 80 см²

#SPJ5