ПОМОГИТЕ СРОЧНО
ОТМЕЧУ КАК ЛУЧШЕЕ РЕШЕНИЕ ЕСЛИ БУДУТ ВСЕ ОТВЕТЫ
НУЖЕН ТОЛЬКО ОТВЕТ БЕЗ РЕШЕНИЯ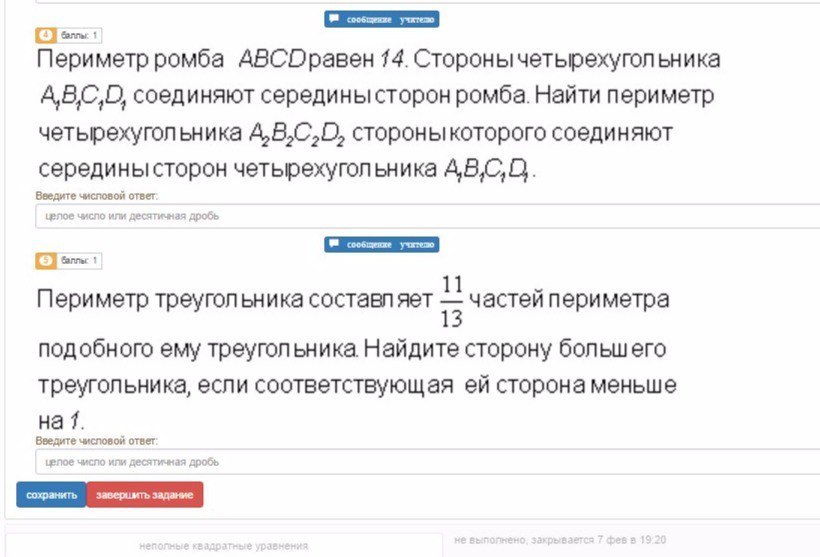

Ответ: 7 см

Интересная задача.В1В=14:4:2=1.75В1В=ВС1(так как стороны в ромбе равны, а В1 и С1 их середины) => В1ВС1 -равнобедренный => угВВ1С1=угВС1В1=а В треугольниках ВВ1С1 и А1Д1Д В1В=А1Д (так как стороны в ромбе равны, а В1 и А1 их середины)ДД1=ВС1 (так как стороны в ромбе равны, а Д1 и С1 их середины0угВ=угД(так как противоположные углы ромбы равны) Отсюда ВВ1С1=А1Д1Д => угД1А1д=угА1Д1д=угВВ1С1=угВС1В1=аа=(180-х)/2(По теореме о сумме углов в равнобедренном В1ВС1)Анологично и В треугольниках АВ1А1 и СС1Д1 В1А=С1С (так как стороны в ромбе равны, а В1 и С1 их середины)АА1=СД1 (так как стороны в ромбе равны, а Д1 и А1 их середины0угА=угС(так как противоположные углы ромбы равны) Отсюда АВ1А1=СС1Д1 => угАВ1А1=угСС1Д1д=угС1Д1С=угВ1А1А=вв=(180-у)/2(По теореме о сумме углов в равнобедренном В1АА1)Но мы знаем, что сумма двух непротивоположных углов в ромбе равна 180:х+у=180 тогдаа+в=90-0.5х+90-0.5у=180-0.5(х+у)=90Теперь можно найти угол А1В1С1=180-(а+в)=90; В1А1Д1=180-(а+в)=90 ЗНАЧИТ а1в1с1д1 - прямоугольник = В1С1=В1А1=С1Д1=Д1А1, а такж и отрезки разделенные серединами равныВ треугольнике В1ВС1, В1С2- будет медианой, высотой и биссектрисой, тогда имеем в прямоугольном В1ВВС2, В1С2=cosa*B1B=1.75*сosaТАКЖЕ и в АВ1В2, В1В2=1.75cosb=1.75sina(т к а+в=90)теперь наконец рассмотрим прямоугольный В2В1С2 по т пифагораB_{2}C_{2}=\sqrt{(B1C2)^2+(B1B2)^2}=\sqrt{1.75^2(sin^2a+cos^2a)}=1.75P=4*В2С2=7смОтвет 7 см