В треугольнике abc известно что ab=bc, ac = 8 см, AD - медиана, BE - высота, BE = 12 см, Из точки D опущено перпендикуляр DF на сторону AC. Найдите отрезок DF и угол ADF.

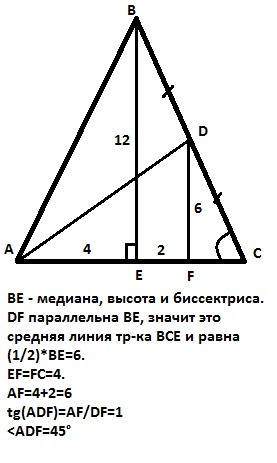
В треугольнике abc известно что ab=bc, ac = 8 см, AD - медиана, BE - высота, BE = 12 см, Из точки D опущено перпендикуляр DF на сторону AC. Найдите отрезок DF и угол ADF. ВЕ - высота равнобедренного треугольника, значит ВЕ - медиана этого треугольника.АЕ=ЕС. DF - перпендикуляр к АD, то есть DF параллельна ВЕ и является средней линией треугольника ВЕС, так как точка D - середина стороны ВС (АD- медиана - дано). ТогдаDF=(1/2)*BE=6 см. ЕF=(1/2)*ЕС или EF=8:2=4см. AF=АЕ+ЕF или АF=4+2=6. Тангенс угла ADF - это отношение противолежащего катета к прилежащему, то есть td(ADF)=AF/DF=1. <ADF=45°.Ответ: отрезок DF=6см, <ADF=45°.