Диагонали ромба равны 3 и 4 найти синус угла между большей диагональю и стороной ромба

Ответ:

sin\alpha =0,6.

Объяснение:

Диагонали ромба равны 3 и 4. Найти синус угла между большей диагональю и стороной ромба.

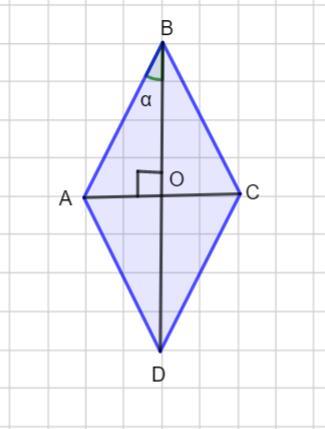
Пусть дан ромб АВСD

Диагонали ромба АС = 3 ед. ВD = 4 ед.

Диагонали ромба пересекаются в точке О и точкой пересечения делятся пополам.

Тогда АО=ОС =3 : 2 = 1,5 ед. ВО =ОD= 4 : 2 =2 ед.

Диагонали ромба пересекаются под прямым углом .

ΔАОВ - прямоугольный. Найдем гипотенузу АВ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

AB ^{2} =AO^{2} +OB^{2} ;\\AB= \sqrt{AO^{2} +OB^{2}} ;\\AB =\sqrt{(1,5)^{2} +2^{2} } =\sqrt{2,25+4} =\sqrt{6,25} =2,5

Пусть ∠АВО =α - это угол между большей диагональю ромба и его стороной.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета  к гипотенузе.

sin\alpha =\dfrac{AO}{AB} ;\\\\sin\alpha =\dfrac{1,5}{2,5} =\dfrac{1,5\cdot2}{2,5\cdot2}=\dfrac{3}{5} =0,6

#SPJ5