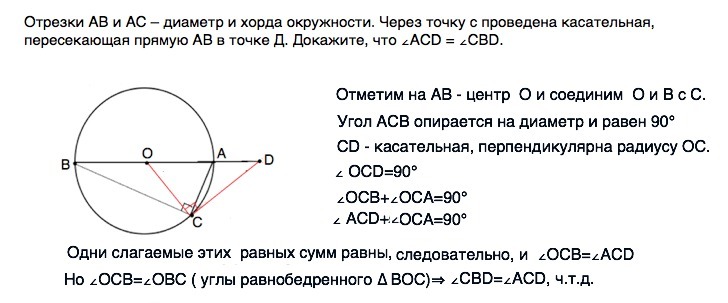
Отрезки АВ и АС – диаметр и хорда окружности. Через точку с проведена касательная, пересекающая прямую АВ в точке Д. Докажите, что ∠АСD = ∠СВD.

Отметим на АВ - центр  О и соединим  О и В с С.

Угол АСВ опирается на диаметр и равен 90°

СD - касательная, перпендикулярна радиусу ОС. 

 ∠ OCD=90°

∠ОСВ+∠ОСА=90°

∠ ACD+OCA=90°

Одни слагаемые этих  равных сумм равны, следовательно, и  ∠ОСВ=∠ACD Но ∠ОСВ=∠ОВС ( углы равнобедренного ∆ ВОС)⇒∠СВD=∠АСD, ч.т.д.

--------

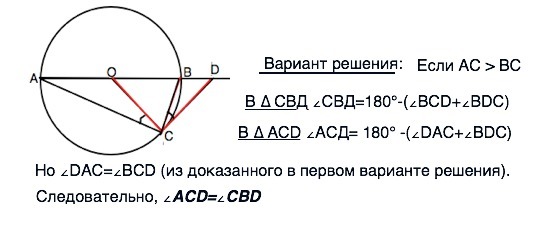
Вариант решения:  

Если АС > ВС

В ∆ СВД ∠СВД=180°-(∠ВСD+∠ВDС)

В ∆ АСD ∠АСД= 180° -(∠DAC+∠BDC)

Но ∠DАС=∠BCD (из доказанного в первом варианте решения). 

Следовательно, ∠ACD=∠CBD