основания равнобедренной трапеции равны 8 и 6, высота равна 7. найдите радиус описанной окружности

Ответ: R=5 (ед. длины)

Объяснение:

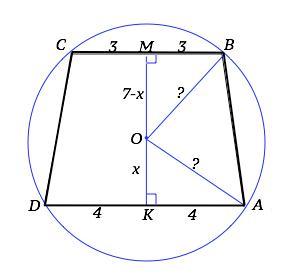
  Обозначим трапецию АВСD и сделаем рисунок.

Пусть О  – центр описанной окружности, МК =7 - высота трапеции, проходящая через т. О.

Так как ОМ  и ОК перпендикулярны основаниям, а отрезок из центра окружности, перпендикулярный хорде, делит ее пополам (свойство), то СМ=МВ=3, DК=КА=4 .

Пусть ОК=х. Тогда ОМ=7-х.

ОВ=ОА – радиусы.

Выразим по т. Пифагора квадраты ОВ и ОА из прямоугольных треугольников МОВ и КОА и приравняем их:

ОА²=ОК²+КО²

ОВ²=ОМ²+МВ² ⇒  ОК²+КА² =ОМ²+МВ²

х²+4²=(7-х)²+3²

Решив уравнение, получим ². Отсюда ∆ МОВ=∆ КОВ с катетами 3 и 4 – египетские, их гипотенузы=R=5 (ед. длины)