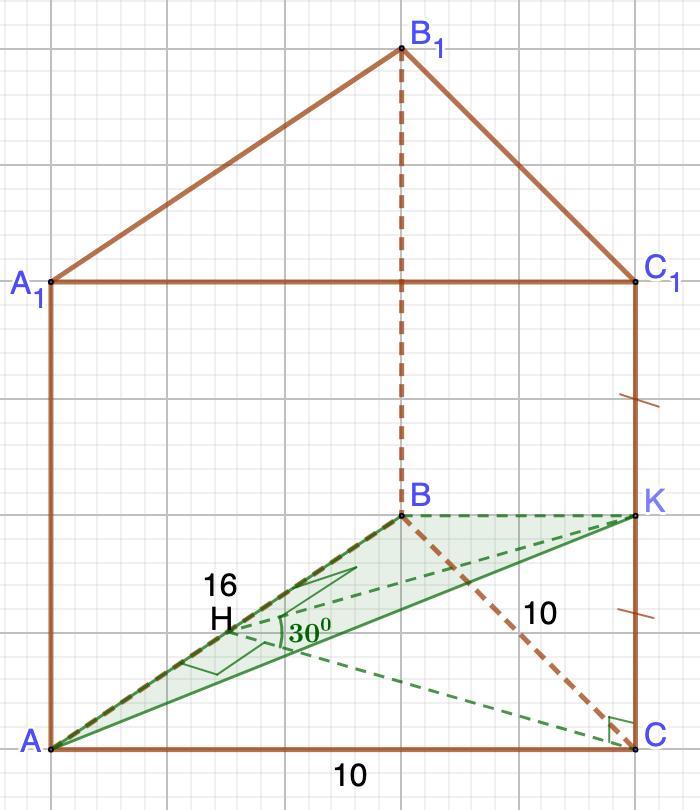
Основанием прямой призмы является треугольник со сторонами 10см,10см и 16 см. Через большую сторону нижнего основания и середину противоположного бокового ребра проведена плоскость под углом 30° к плоскости основания. Найдите объем призмы.

Ответ:

192√3 см³

Объяснение:

Дано: АВСА₁В₁С₁ - прямая призма.

АВ=16 см; АС=ВС=10 см;

∠КНС = 30°.

СН=С₁Н.

Найти: V призмы.

Решение:

1. Рассмотрим ΔАВС - равнобедренный.

В равнобедренном треугольнике высота является медианой.

⇒ АН = НВ =АВ:2 = 16:2 = 8 (см)

Найдем высоту СН по теореме Пифагора:

СН² = АС²-АН² = 100-64 = 36 ⇒ СН=6 (см)

2. Рассмотрим ΔНКС - прямоугольный.

∠КНС = 30°

Катет, лежащий против угла в 30°, равен половине гипотенузы.

Пусть КС = х, тогда НК = 2х.

По теореме Пифагора:

НС² + СК² = НК²  ⇒  36 + х² =  4х² ⇒ х² = 12;

х = 2√3 (см)

СК = 2√3 см  ⇒  СС₁ = 4√3 см.

3. Найдем площадь основания и объем призмы.

Площадь треугольника равна половине произведения основания на высоту.

\displaystyle S_{OCH}=\frac{1}{2}AB*HC=\frac{1}{2}*16*6=48 \;_{(CM^2)}

Объем призмы равен произведению площади основания на высоту.

V призмы=S осн.·СС₁=48·4√3=192√3 (см³)