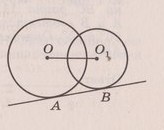
К двум пересекающимся окружностям радиусов 12 и 4 см проведена касательная. Найдите расстояние между центрами окружностей, если отрезок АВ касательной равен 17 см.

Т.к. АВ - касательная в обеим окружностям, то она перпендикулярна ОА и О1В, значит ОА параллельно О1В и значит АВО1О - прямоугольная трапеция. Из точки О1 опустим перпендикуляр О1С на сторону ОА и получим прямоугольный треугольник СОО1 и прямоугольник АВО1С. О1С = АВ = 17;  АС = ВО1 = 4.

Рассмотрим треугольник СОО1: СО=ОА-СА=ОА-ВО1=12-4=8. По теореме Пифагора ОО1^2=CО^2+O1C^2=8^2+17^2=64+289=353/

Ответ: ОО1 = корень из 353