-
Задача по геометрии..
Помогите решить)
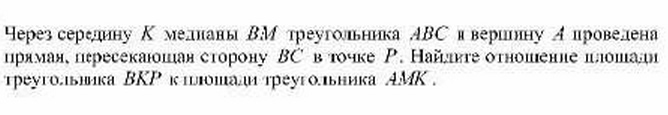
-
Предмет:
Геометрия -
Автор:
georgeeiid - 6 лет назад
-
Ответы 1
-
Решение к этой задаче дается разное, и часто копируется друг у друга как верное, так и ошибочное.
У этой задачи два варианта: найти отношение треугольников и отношение треугольника и четырехугольника.
Эта задача требует найти отношение S ᐃ ВКР и S ᐃАМК.
S ᐃ ВКР=S ᐃ ВАР - S ᐃ ВАК
S ᐃ ВАК=S ᐃ ВАМ:2S ᐃ ВАМ=S ᐃ АВС:2
Площадь треугольника АВМ равна половине площади ᐃ АВС, так как основания их относятся как 1:2 , а высоты равны - (ВМ-медиана и делит АС на две равные части). Площадь ᐃ АВК равна половине площади ᐃ АВМ по тому же основанию: ВК=КМ, а высота из А к ВМ одна и та же для обоих треугольников. Следовательно,
S ᐃ АВК=S ᐃ АКМ=1/2 S ᐃ АВМ=1/4 ᐃ SАВС
Проведем из вершины В прямую ВЕ, параллельную АС. Продолжим АР до пересечения с ВЕРассмотрим треугольники ВКЕ и АКМ. Они равны по стороне и двум углам, прилегающим к ней:
ВК=КМ по условию, вертикальные углы при К равны,
углы КВЕ и КМА равны как накрестлежащие при параллельных ВЕ и АМ и секущей ВМ .Следовательно, ВЕ=АМ=АС:2 ( именно это отношение нам для решения важно)
Сравним треугольники ВРЕ и АРС. Они подобны по трем углам (ВЕ||АС и накрестележащие углы при них равны, вертикальные углы при Р также равны). Так как мы нашли, что ВЕ=АС:2, коэффициент подобия этих треугольников равен 1:2Тогда ВР:РС=1:2Отсюда сторона ВР:ВС=1:3
(ВС=ВР+РС=1 ВР+2 ВР=3 ВР)Так как в треугольниках АВР и АВС высота из вершины А к стороне ВС одна и та же, отношение их площадей равно отношению их оснований. Отношение оснований ВР:ВС=1/3Площадь ᐃ АВР=1/3 площадиᐃ АВС. Тогда:S ᐃ ВКР=S ᐃ АВР - S ᐃ АВК S ᐃ АВК=1/4 S ᐃ АВСS ᐃ АВР=1/3 S ᐃ АВСS ᐃ ВКР=⅓ ᐃ SАВС - ¼ S ᐃ АВС= ¹/₁₂ S ᐃ АВСS ᐃ ВКР:S ᐃАМК= ¹/₁₂ S ᐃ АВС:1/4 S ᐃ АВС=1/3

-
Автор:
lady gaga - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Гигиену относят к социальным наукам, потому что она...
А) изучает болезни ,бытующие в данной местности
Б) исследуют микробный состав воды и пищевых продуктов
В)определяет возможности человека приспосабливаться к новым условиям труда и быта
C)охраняют здоровье людей , живущих на данной территории и работающих на предприятиях одной отрасли производства-
Предмет:
Биология -
Автор:
moonshineaqjg - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
решите плиззз))) (729*8+729*492)/90*(520800/400-498) по действиям и действия напишите))
-
Предмет:
Математика -
Автор:
georgina - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Установите соответствие между исходными веществами и продуктами реакции:
исходное вещество продукты реакции
А)H3PO4+Na2S-> 1)не взаимодействуют
Б)H3PO4+NaOH-> 2)H2S+NaPO4
В)H3PO4+Na2SO4-> 3)Na3PO4+H2O
4)H2SO4+Na3PO4
5)Na3PO4+H2O
-
Сравнительная характеристика общения и коммуникации желательно в форме таблицы
-
Предмет:
Обществознание -
Автор:
spence - 6 лет назад
-
Ответов:
1 -
Смотреть
-
