-
Основанием пирамиды служит равнобедренная трапеция, основания которой равны 2 и 8 см. Боковые грани наклонены к основанию под углом 60°. Найдите высоту пирамиды и площадь её боковой поверхности.
Вот рисунок и дано: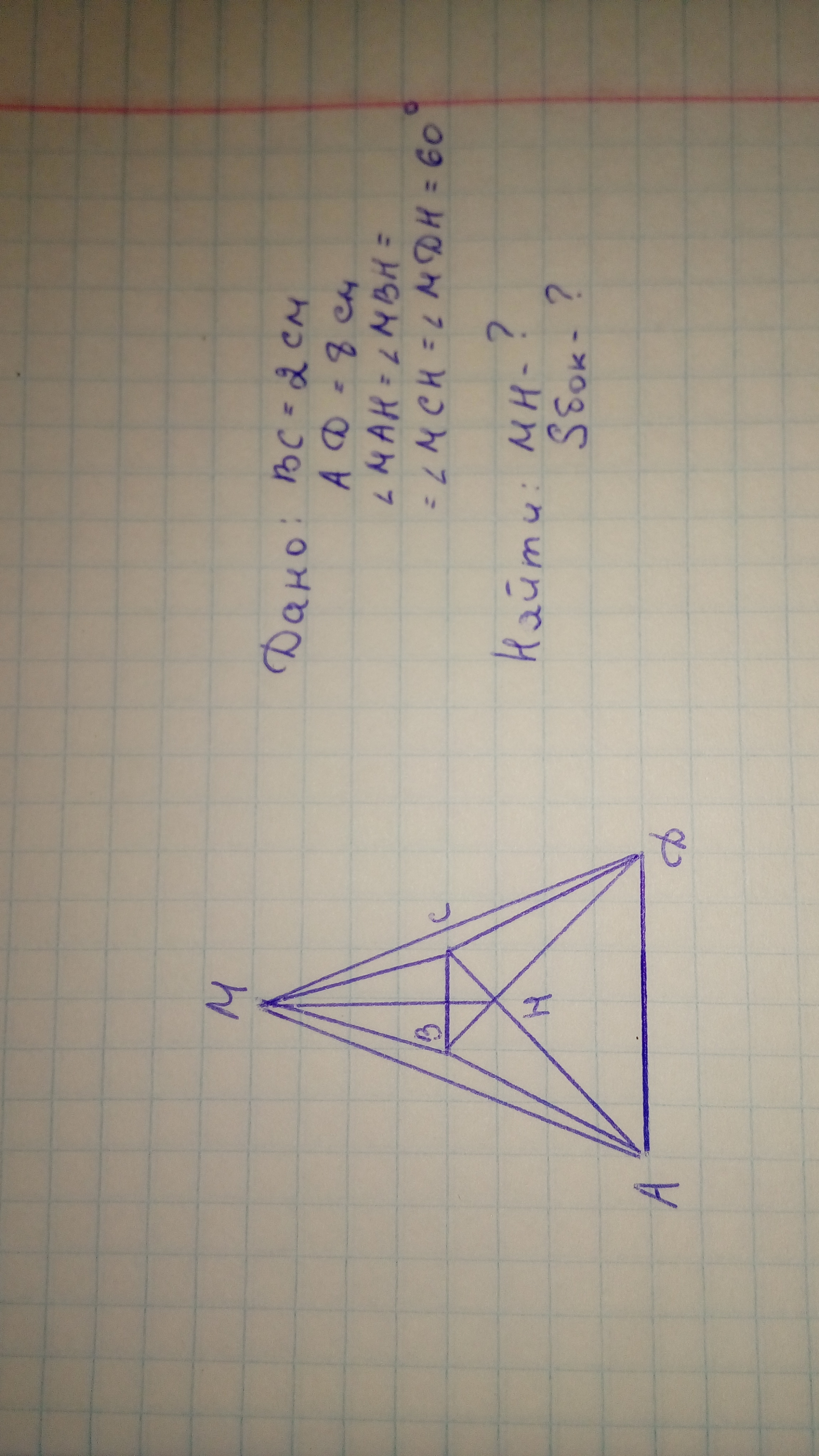
Ответы 3
-
другого решения нет, но я Вам говорю, что у Вас неправильно
-
Автор:
alice61 - 6 лет назад
-
0
-
-
Ваша задача решена ответ можете посмотрет в вложение

-
Автор:
bunnykeh3 - 6 лет назад
-
0
-
-
Трапеция ABCD, основания AD=a=8; BC=b=2, боковые ребра AB=CD=c, высота пирамиды SO=H. Поскольку грани наклонены под одинаковыми углами, апофемы h всех граней равны, и проекции апофем на основание равны⇒ O- центр вписанной окружности⇒a+b=2c⇒c=5. Опустив перпендикуляр BE на AD, получаем прямоугольный треугольник ABE с AB=5; AE=(AD-BC)/2=3⇒BE=4⇒радиус вписанной окружности, он же проекция любой апофемы на основание = 2. Поскольку высота пирамиды, одна из апофем и проекция апофемы на основание образуют прямоугольный треугольник с острыми углами 30° и 60°⇒апофема в два раза больше радиуса⇒h=4⇒S_(бок)=(1/2)P_(осн)·h=(1/2)(8+2+5+5)·4=40; H=2√3Ответ: 40

-
Автор:
ruffe - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
А1. Йод с солью относится:
1 ) к гомогенным системам
2) к простым веществам
3) к гетерогенным системам
4) к химическим соединениям-
Предмет:
Химия -
Автор:
chipperojf3 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
в зависимости от степени нанесённого вреда правонарушения делятся на
1.уголовные преступления
2. административные проступки
3. международные преступления
4. гражданские правонарушения-
Предмет:
Обществознание -
Автор:
marques - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Сократите дробь 45/54
-
Предмет:
Математика -
Автор:
mccormick - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
На лестнице фонарщика 8 ступеней, он всегда забирается на верхнюю.
На сколько ступеней ему надо подняться , чтобы зажечь 20 фонарей?
Даю 95 баллов-
Предмет:
Другие предметы -
Автор:
missyghic - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
