Вычислите объем правильной четырехугольной усеченной пирамиды со сторонами основания 7 и 9 см, а боковое ребро наклонено к плоскости основания под углом 30 градусов.

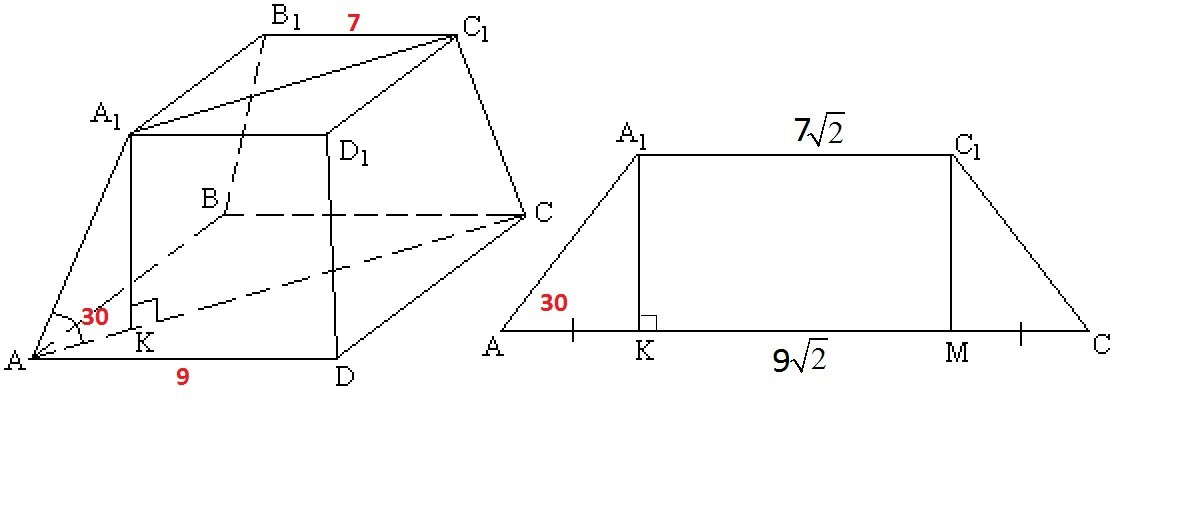
ABCDA_1B_1C_1D_1- правильная четырехугольная усеченная пирамидаB_1C_1=7 смAD=9 см\ \textless \ A_1AC=30кV_n - ?Так как ABCDA_1B_1C_1D_1  правильная пирамида, то её основания являются квадратами ABCD и A_1B_1C_1D_1- квадратыAB=BC=CD=AD=9 смA_1B_1=B_1C_1=C_1D_1=A_1D_1=7 смd=a \sqrt{2}  AC=9 \sqrt{2} смA_1C_1=7 \sqrt{2} смсделаем выносной рисунок:AA_1C_1C- равнобедренная трапеция AA_1=CC_1A_1K ⊥ ACC_1M ⊥ ACKA_1C_1M- прямоугольникA_1C_1=KM=7 \sqrt{2} смΔ AA_1K- прямоугольныйΔ CC_1M- прямоугольныйΔ AA_1K= Δ CC_1M ( по двум углам)AK=MC= \sqrt{2} см \frac{A_1K}{AK} =tg\ \textless \ KAA_1{A_1K}={AK} *tg\ \textless \ KAA_1{A_1K}={ \sqrt{2} } *tg\ \textless \ 30к{A_1K}={ \sqrt{2} } * \frac{ \sqrt{3} }{3} = \frac{ \sqrt{6} }{3} V_n= \frac{1}{3} H(S_1+ \sqrt{S_1*S_2} +S_2)S_1=7^2=49 см²S_2=9^2=81 см²V_n= \frac{1}{3} *\frac{ \sqrt{6} }{3}(49+ \sqrt{49*81} +81)V_n= \frac{ \sqrt{6} }{9}(130+ 7*9)V_n= \frac{ \sqrt{6} }{9}*193V_n= \frac{193 \sqrt{6} }{9} cм³Ответ: \frac{193 \sqrt{6} }{9} см³чертеж в приложении