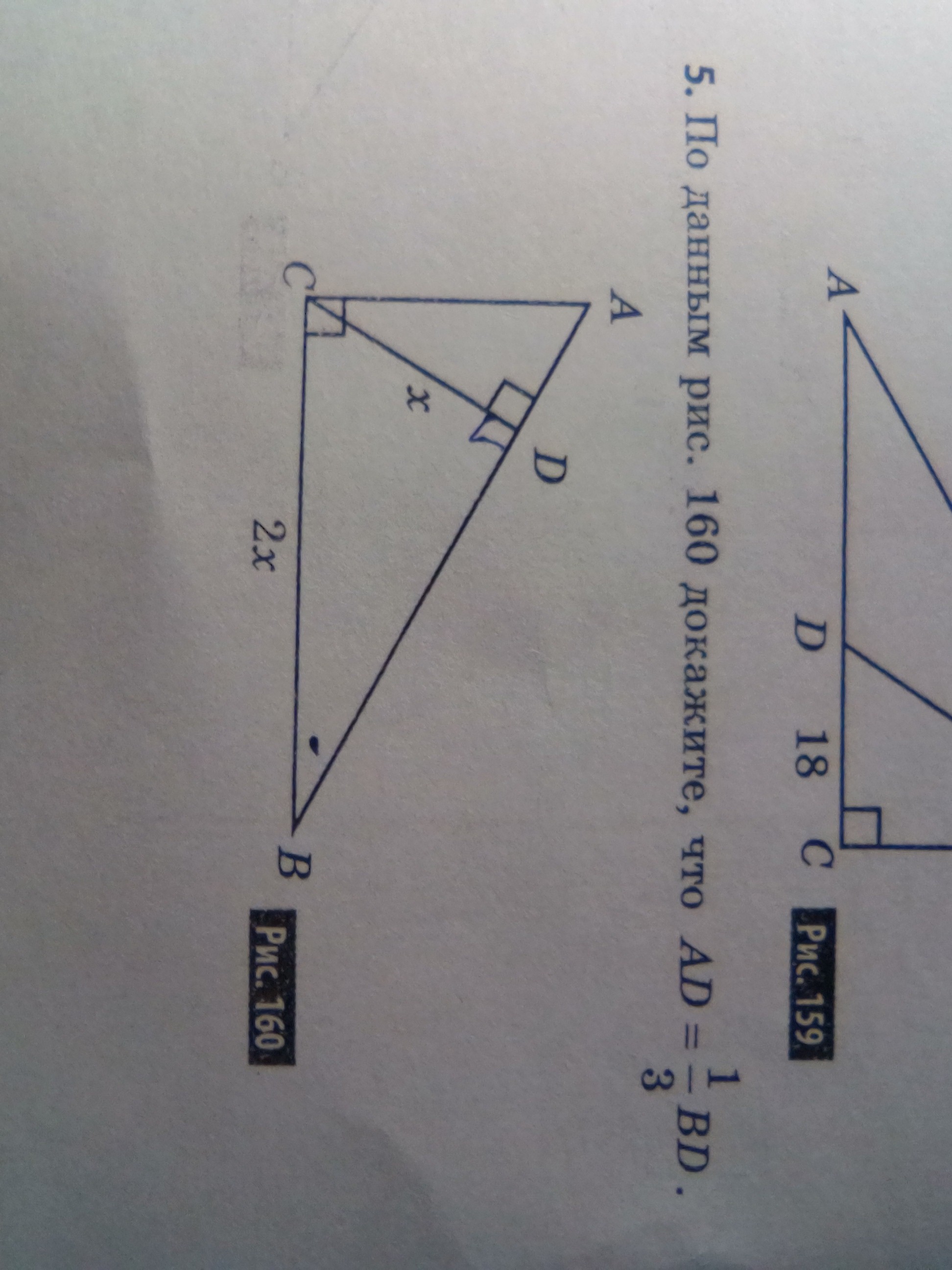
Помогите по данным рисунка доказать что AD=1/3BD. Умоляю!

Ответы 1

Р/м треугольник СДВ. ∠Д=90, СВ=2х, СД=х (по условию) отсюда следует по с-ву угла в 30*, что ∠В=30*, так как противолежащая сторона (СД)=2 гипотенузам (СВ).Р/м треугольник АВС, где ∠С=90*, ∠В=30*, отсюда следует по свойству углов в треугольнике, что ∠А=60* (180-90-30).Р/м треугольник АДС. ∠Д=90*, ∠А=60*, следовательно, ∠С=30*, отсюда уже следует, что треугольники АДС и АВС подобны по трем углам.Вновь р/м треугольник АДС. По с-ву угла в 30* следует, что АД=1/2АСПо т. Пифагора получаем уравнение, в котором у = АД, 2у=АС $x^{2} = y^{2} - (2y)^{2} =3 y^{2}$ $x= \sqrt{3 y^{2}} = y \sqrt{3}$ Теперь р/м т. Пифагора для треугольника ВСД, где z = ДВ, а $х= y \sqrt{3}$ $4x^{2} - x^{2} = z^{2}$ $3 x^{2} = z^{2}$ $z= \sqrt{3 x^{2} } = \sqrt{3* (y \sqrt{3})^{2} } = \sqrt{3* y^{2}*3 } = \sqrt{9 y^{2} } =3y$ т.к у - это обозначение для АД, а z для ДВ, то следовательно, 3АД=ДВ или АД=1/3ДВ
- Автор:
  konnorp9sr
- 5 лет назад
- 0
Добавить свой ответ