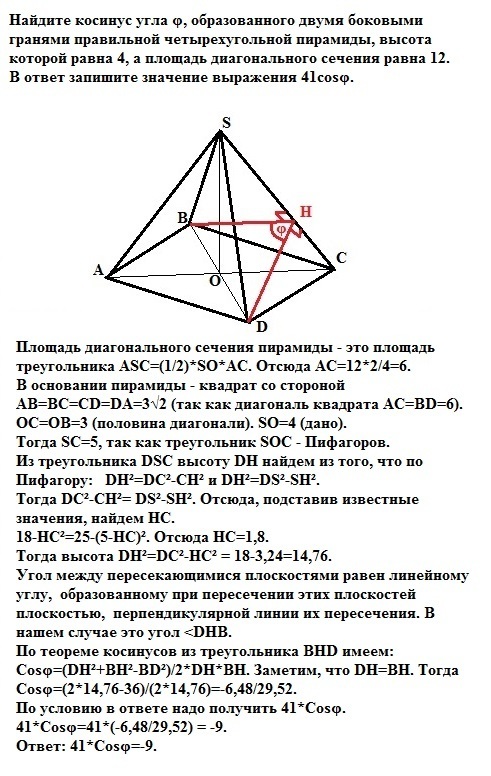
Найдите косинус угла φ, образованного двумя боковыми гранями правильной четырехугольной пирамиды, высота которой равна 4, а площадь диагонального сечения равна 12. В ответ запишите значение выражения 41cosφ

Площадь диагонального сечения пирамиды - это площадь треугольника АSC=(1/2)*SO*AC. Отсюда АС=12*2/4=6.В основании пирамиды - квадрат со стороной АВ=ВС=СD=DA=3√2 (так как диагональ квадрата АС=BD=6).OC=OB=3 (половина диагонали). SO=4 (дано). Тогда SC=5, так как треугольник SOC - Пифагоров.Из треугольника DSC высоту DH найдем из того, что по Пифагору: DH²=DC²-CH² и DH²=DS²-SH². Тогда DC²-CH²= DS²-SH². Отсюда, подставив известные значения, найдем НС.18-НС²=25-(5-НС)²  =>  НС=1,8.Тогда DН²=DC²-НС² = 18-3,24=14,76.Угол между пересекающимися плоскостями равен линейному углу, образованному при пересечении этих плоскостей плоскостью, перпендикулярной линии их пересечения. В нашем случае это угол <DHB.По теореме косинусов из треугольника ВНD имеем:Cosφ=(DH²+BH²-BD²)/2*DH*BH. Заметим, что DH=BH. ТогдаCosφ=(2*14,76-36)/(2*14,76)=-6,48/29,52.По условию в ответе надо получить 41*Cosφ.41*Cosφ=41*(-6,48/29,52) = -9.Ответ: 41*Cosφ=-9.