-
Постройте две окружности радиусов 3 и 2 см, пересекающиеся в двух точках A и B. При помощи циркуля и линейки построить точку M середину отрезка AB. Лежат ли центры окружностей и точка М на одной прямой? Докажите.
Помогите доказать! Пожалуйста
Даю 30 баллов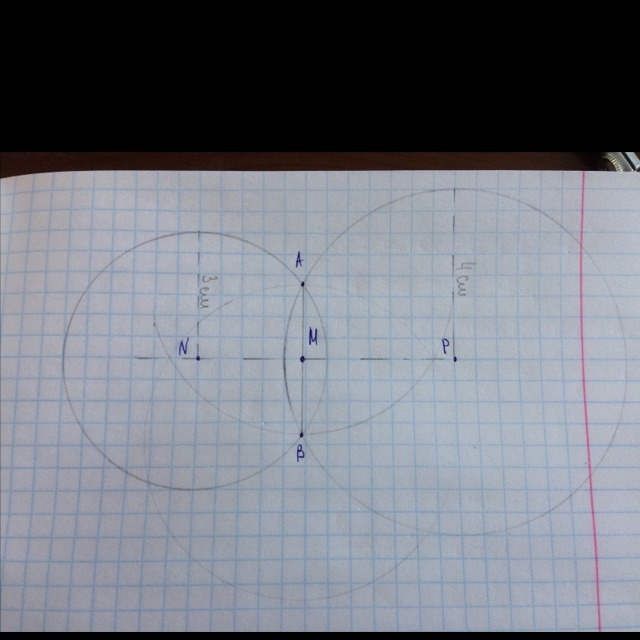
-
Предмет:
Геометрия -
Автор:
boomhauerrntb - 5 лет назад
-
Ответы 1
-
1. Построение точки середины отрезка АВ:Из точек А и Р радиусом АР проводим две окружности.Соединяем точки их пересечения отрезком РР1.На пересечении этого отрезка с отрезком АВ получаем точку М - середину отрезка АВ.2. Докажем, что точка М лежит на прямой, соединяющей центры N и P данных окружностей:АМ=МВ по построению. В треугольнике ANB отрезок NM - медиана. Треугольник равнобедренный, так как АN=BN (радиусы).Следовательно, NM - высота этого треугольника.Точно так же отрезок РМ - высота треугольника АРВ.Итак, NM - перпендикуляр к АВ и РМ - перпендикуляр к АВ, точка М - общая.Из точки на прямой (М) можно провести только одну прямую, перпендикулярную к этой прямой, следовательно NM и РМ лежат на одной прямой.То есть точки N,М и Р лежат на одной прямой, что и требовалось доказать.

-
Автор:
davies - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- как изменения в экономике советского тыла повлияли на характер войны и одержанные победы
-
Вычислите сумму в столбик
18,62+7,389 40,396+8,7
-
Предмет:
Математика -
Автор:
anthonydavis - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите решить уравнение 937 - 8x= 681
-
Предмет:
Математика -
Автор:
daviddzet - 5 лет назад
-
Ответов:
4 -
Смотреть
-
-
Исследуйте и постройте график данной функции.
y = x^3 - 12x + 5
How much to ban the user?
1 hour
1 day
100 years
