-
Пожалуйста помогите решить задачу по геометрии
Не игнорьте
Даю 60 баллов за бистрий ответ!
Центры круга и правильного треугольника, изображенных на рис.47, совпадают. Сторона треугольника = 10 * корень из 3. Длина хорды АВ = радиусу окружности, описанной около треугольника. Найдите площадь заштрихованной фигуры.
Рисунок во вложении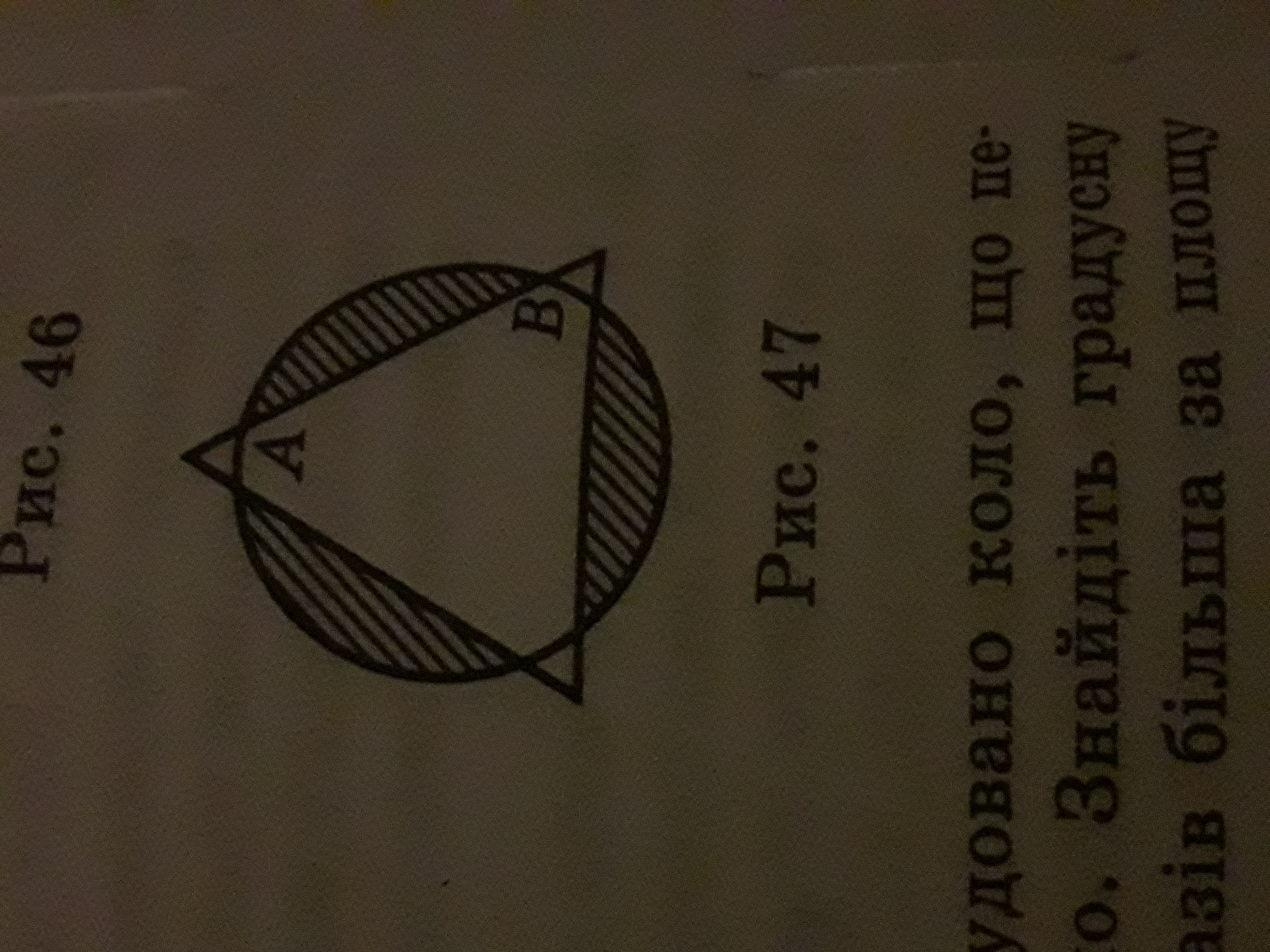
-
Предмет:
Геометрия -
Автор:
damianwtny - 6 лет назад
-
Ответы 1
-
ΔKMP - правильный, КМ=10√3, АВ=КМ.Радиус большей окружности: ОК=R=КМ/√3=10√3/√3=10.ОН - радиус вписанной окружности в тр-ник КМP. r=R/2=5.В равнобедренном тр-ке АОВ ОН⊥АВ, значит ОН - медиана. АН=НВ=АВ/2=5.В прямоугольном тр-ке АОН АО=АН, значит он равнобедренный, значит ∠АОН=45°, следовательно ∠АОВ=90° (треугольники АОН и ВОН равны по трём сторонам).АО=АН√2=5√2.Формула площади сегмента окружности: S=((π·α°/180°)-sinα)·R²/2.Площадь заштрихованного сегмента, ограниченного хордой AB, окружности с радиусом АО:S=((π·90/180)-sin90)·(5√2)²/2=((π/2)-1)·50/2=25(π-2)/2.Так как окружности с радиусами ОК и ОА концентрические и треугольник КМP правильный, то заштрихованные сегменты равны.Площадь всех заштрихованных сегментов (площадь искомой фигуры):Sф=3S=75·(π-2)/2 (ед²)- это ответ.

-
Автор:
cutie pie - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Здравствуйте! Может вы знаете что-нибудь о Родольфе Бонетто ( итальянский дизайнер 20 века). Ничего не могу найти о нем!
-
Предмет:
МХК -
Автор:
silviarcwg - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
В рассказах Н.В.Гоголя :"Вечера на хуторе близ Диканьки","Вий","Ночь перед Рождеством","Вечер на кануне Ивана Купалы",имеется ли фантастика и фольклор?И какие волшебные предметы и персонажи наделенные сверхъестественной силой,действуют в них?
-
Предмет:
Литература -
Автор:
sophiaosborn - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Металл массой 13,7 г, что образует катион с зарядом 2, реагирует с водой с выделением 2,24 л водорода. Назовите этот металл.
- 30 баллов. полное решение логарифмического неравенства 7.92 - 2)
How much to ban the user?
1 hour
1 day
100 years
