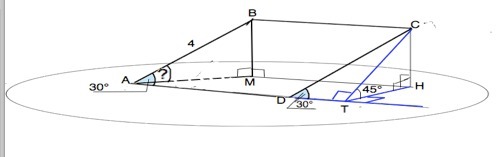
8. Параллелограмм ABCD наклонен к плоскости ,бета под углом 45º. AD лежит в плоскости бета, причем AB = 4 см, угол BAD = 30º.
Найдите угол между стороной AB и плоскостью бета.

Искомый угол - угол ВАМ  в ∆ ВАМ,  где ВМ и АМ- катеты, АВ - гипотенуза. 

Проведем высоту параллелограмма - перпендикуляр СТ к продолжению АD. 

CD=AB=4, угол СDТ=углу ВАD=30° 

СТ=СD• sin30° =4•1/2=2 

СН ⊥плоскости β,  НТ⊥DТ. 

∠СТН=45° по условию, откуда СН=2•sin45°=√2

ВС параллельна плоскости β, все ее точки одинаково удалены от неё. 

ВМ=СН=√2

sin BAM=BM:AB=(√2):4=0,35355 

Ответ: arcos 0,35355 . Это угол 20°42'