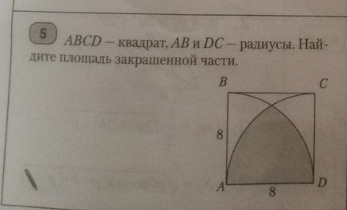
ABCD-квадрат, АВ и DC-радиусы. Найдите площадь закрашенной части.

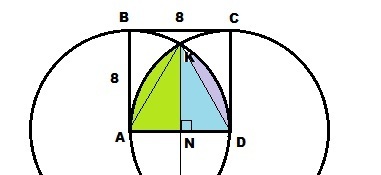
 ABCD - квадрат, ∠BAD = ∠CDA = 90°,  AB = CD = R = 8Нужно найти площадь криволинейной фигуры AKD.Так как окружности имеют одинаковый радиус 8, то фигура AKD симметрична относительно перпендикуляра KN⊥AD. Достаточно найти площадь криволинейной фигуры AKN, половинки AKD.Площадь фигуры AKN равна площади сектора DAK минус площадь прямоугольного треугольника DNKΔAKD - равносторонний - AK = KD = AD = R = 8  ⇒  ∠ADK = 60° Площадь сектора DAK:S_{cDAK} = \frac{ \pi R^2*60^o}{360^o} = \frac{ \pi *8^2}{6} = \frac{32 \pi }{3} ΔDNK - прямоугольный: ∠ADK = 60°; DK=R=8;  ND=R/2=4S_{DNK}= \frac{1}{2} DK*ND*sin60^o= \frac{1}{2} *8*4* \frac{ \sqrt{3} }{2} =8 \sqrt{3} Площадь криволинейной фигуры AKN:S_{AKN}=S_{cDAK}-S_{DNK}= \frac{32 \pi }{3} -8 \sqrt{3}=8( \frac{4}{3} \pi - \sqrt{3} ) \\ \\ S_{AKD}=2*S_{AKN}=16( \frac{4}{3} \pi - \sqrt{3} )Площадь закрашенной части  равна  S = 16(4π/3 - √3)