-
Вычисли радиус окружности, если отрезок касательной
AK=3√3 мм и ∢OAK=30°
OK=?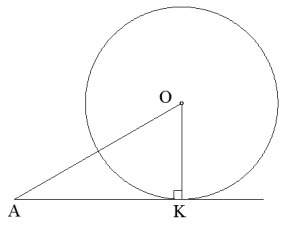
-
Предмет:
Геометрия -
Автор:
madelynbd5k - 5 лет назад
-
Ответы 1
-
Треугольник ОАК прямоугольный т.к. радиус, проведенный в точку касания, перпендикулярен к касательной. Т.к. <OAK =30, то ОК=1/2АО или АО=ОК. Пусть ОК=х, тогда АО=2х. по теореме Пифагора АO^2=AK^2+OK^2
4x^2=27+x^2. 3x^2=27. x^2=9. x=3=OK=R
-
Автор:
jamir - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Напишите сочинение 10 предложений, которое начинается такими словами " Какое сырое утро! За окном мутно. Капает с крыш.
-
Предмет:
Русский язык -
Автор:
glenn82 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
корабль летит со скоростью 8 км/с какое растояние пролетит за 11 с.
-
Предмет:
Математика -
Автор:
flashbeps - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
написать 10 утвердительный и 10 вопросительных предложений в пассивном залоге
-
Предмет:
Английский язык -
Автор:
addison - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- РАССКАЗ О МАРАФонской битве кратко
How much to ban the user?
1 hour
1 day
100 years
