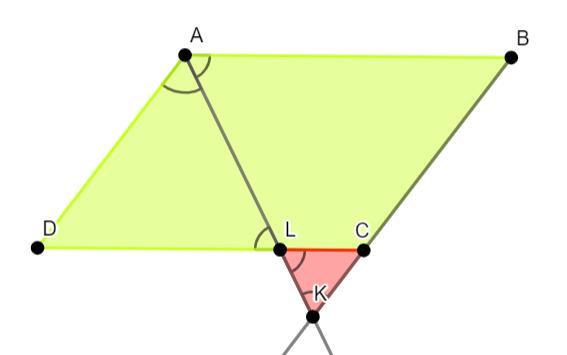
В параллелограмме ABCD биссектриса угла A Пересекает сторону CD в точке L а продолжение стороны BC в точке K. Найти периметр параллелограмма если cl=8 ak=49 периметр треугольника clk = 30.
Прошу распишите по подробнее

• Противоположные стороны параллелограмма параллельны.

⇒ AB║CD;  AD║BC.

AD║KB т.к. K∈BC;

∠KAD = ∠AKB, как внутренние накрест лежащие углы при AD║KB и секущей AK;

∠KAB = ∠KLC, как соответственные углы при AB║LC и секущей AK;

K∈AL ⇒

∠KAB = ∠KAD, как углы при биссектрисе AL;

∠ALD = ∠KLC, как вертикальные углы при AK∩CD;

По итогу мы получили следующее:

∠KAD = ∠KLC = ∠ALD = ∠AKB.

• Стороны треугольника, лежащие напротив равных углов, равны.

В ΔCLK: ∠KLC = ∠LKC  ⇒  CK = LC;

• Периметр треугольника равен сумме его сторон.

P(CLK) = LC+CK+LK;

30 = 2·LC+LK;

LK = 30-2·LC = 30-2·8 = 30-16 = 14.

AK = AL+LK;

49 = AL+14;

AL = 49-14 = 35.

ΔDAL ~ ΔCLK по двум углам (∠DAL=∠CKL и ∠DLA=∠CLK).

• В подобных треугольниках сходственные стороны пропорциональны и лежат напротив равных углов.

⇒ \dfrac{AL}{KL}=\dfrac{DL}{CL};\\\\\dfrac{35}{14} =\dfrac{DL}{8};\\\\DL=8\cdot \dfrac{5\cdot 7}{2\cdot 7}=5\cdot 4=20.

CD = DL+LC = 20+8 = 28;

• Стороны треугольника, лежащие напротив равных углов, равны.

В ΔDAL: ∠DAL = ∠DLA  ⇒  DL = DA;

DA = 20 т.к. DL = 20;

• Периметр параллелограмма в два раза больше суммы его двух смежных сторон.

P(ABCD) = 2·(AD+CD) = 2·(20+28) = 2·48 = 96.

Ответ: 96.