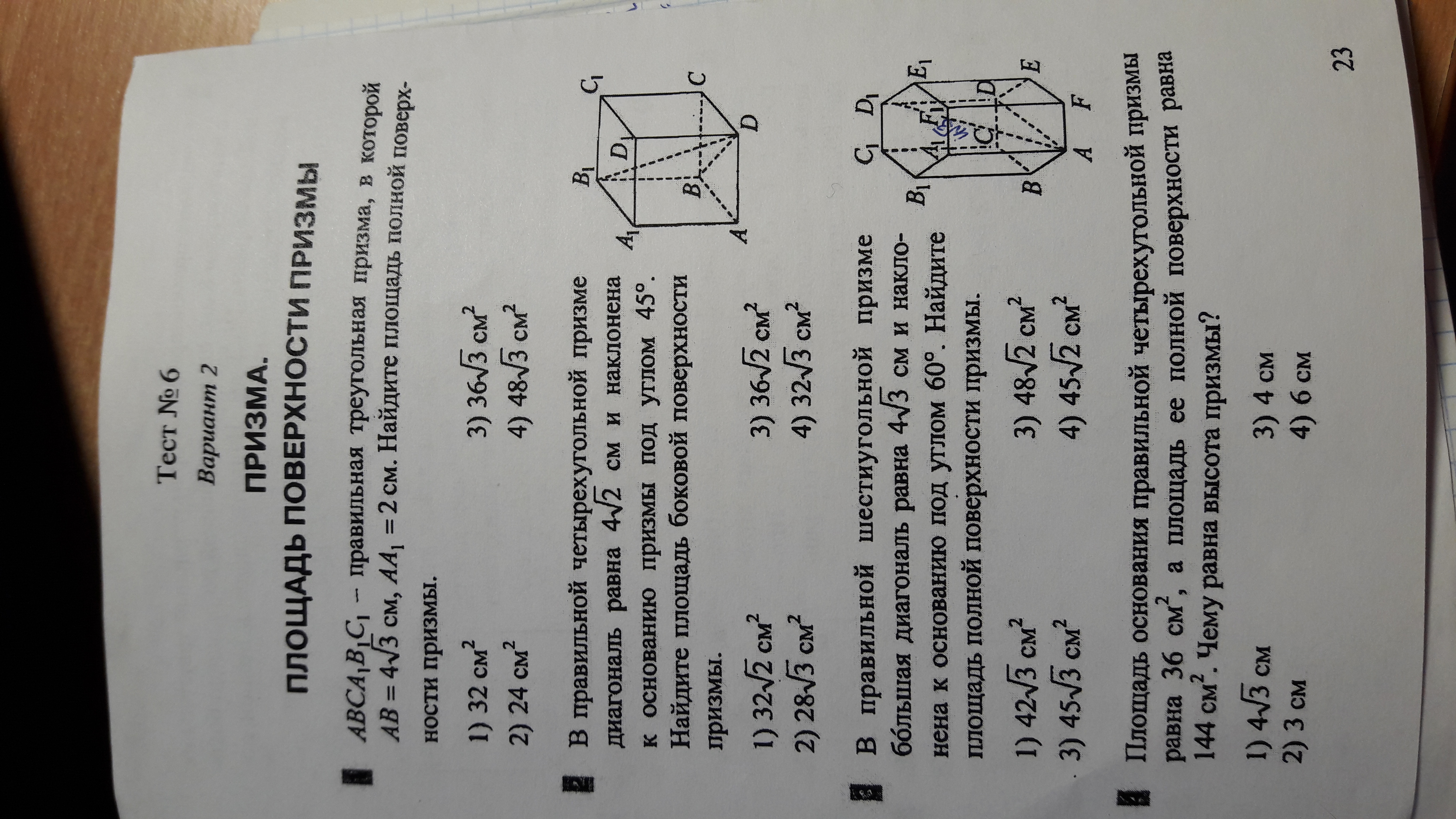
Помогите решить с 1-3 задачи,пожалуйста. Срочно нужно

1.S(основания)= √3/4× а² =(√3/4)×(4(√3)²=12√3S(боковой)=4√3×2=8√3S(полной)=2×12√3+3×8√3=24√3+24√3=48√3Oтвет - 4)2. B1D =4√2, BB1=B1D×sin45°=4BD=4√2×cos45°=4AD=BD×cos45°=4×2√2=8√2AD=BAS(боковой)=8√2×4=32√2Ответ-1)3. В сечении через б. диагональ - прмоугольный 3-угольник с углами 30° и 60°. Нижний катет - половина гипотенузы (4√3/2=2√3) . Большой катет (высота призмы -L) 4к. кв. из 3 на cos30°=6. Сторона 6-угольника равна радиусу в основании (вписаного 6-угольника). Пол-диагонали = √3. S(бок) =р-периметр на высоту=6√3×6=36√3. Два основания 2*S(осн) =2×(3/2)×√3×(√3)²=9√3. Полная S = 36√3+9√3=45√3. Ответ - 3)