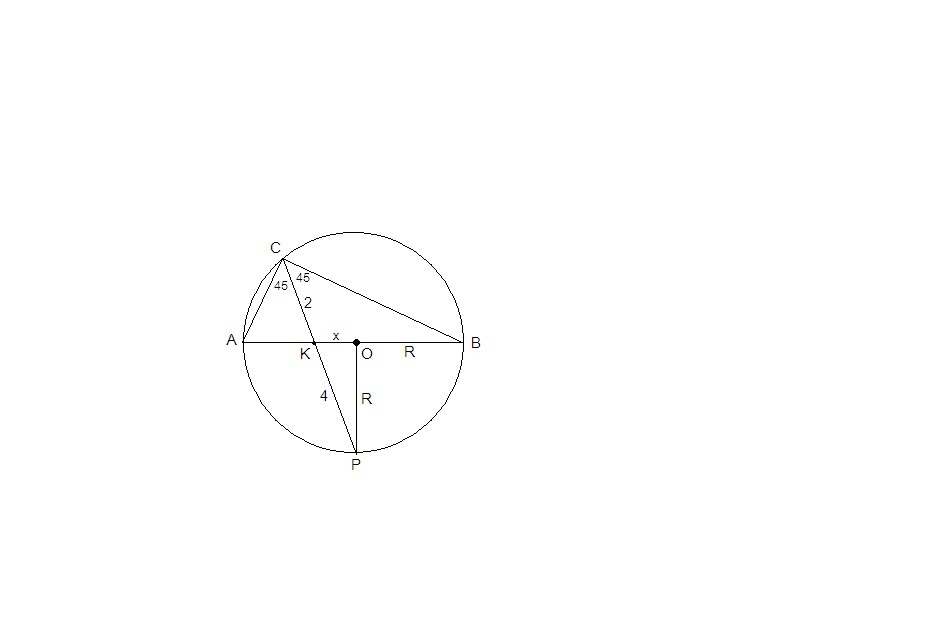
Треугольник ABC прямоугольный, C = 90 градусов. Продолжение биссектрисы CK пересекает описанную около треугольника ABC окружность в точке P, при этом CK = 2, KP = 4. Найти радиус окружности.

∠ACP = 1/2 ∠ACB = 45°. Это вписанный угол, опирающийся на дугу АР. Значит, ∠АОР = 2∠АСР = 90°, как центральный, опирающийся на ту же дугу.ΔОКР: по теореме ПифагораKP² = KO² + OP²16 = R² + x²По свойству отрезков пересекающихся хорд:CK · KP = AK · KB2 · 4 = (R - x) · (R + x)8 = R² - x²Получили систему уравнений:R² + x² = 16R² - x² = 82R² = 24R² = 12R = √12 = 2√3