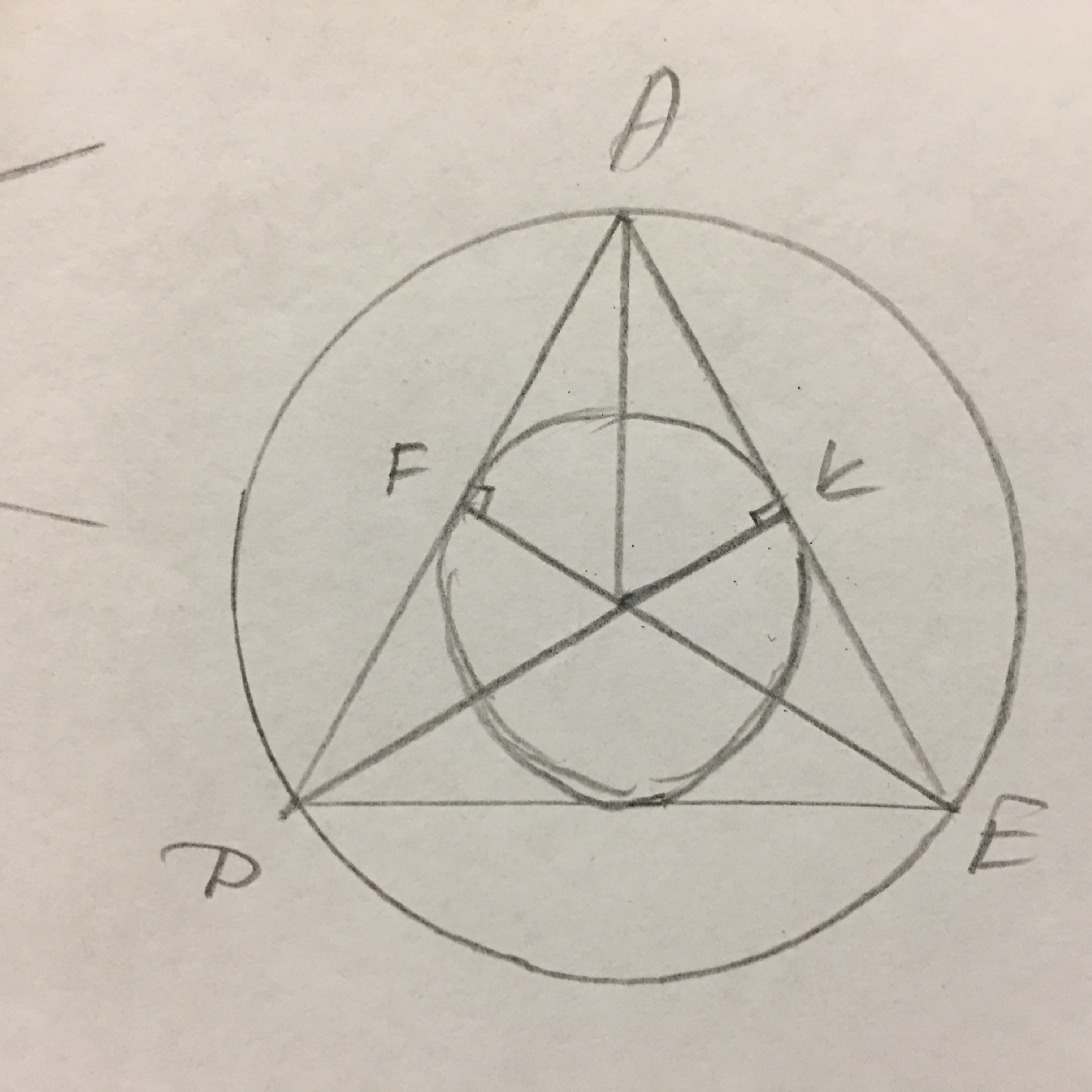
Две концентрические окружности имеют общий центр О. Из произвольной точки А окружности большего радиуса проведены две касательные AF и AK к меньшей,которые пересекают большую окружность в точках D и E соответственно,, угол DAE=60 градусов. Найдите радиус меньшей окружности, если радиус большей равен 8 см

АF=AK как касательные, проведённые из одной точки. OF=OK=R.Треугольники AFO и АКО равны по трём сторонам.Равнобедренные треугольники АОД и AOE равны т.к. ОД=ОЕ, АО - общая сторона, OF=OK ⇒ АК=КЕ и AF=FD ⇒ АЕ=АД.Треугольник АЕД равнобедренный, значит ∠АДЕ=∠АЕД=(180-60)/2=60°.Треугольник АЕД правильный, данные окружности имеют общий центр, бОльшая окружность - описанная, меньшая касается сторон АД и АЕ, значит она вписанная. r=R/2=8/2=4 см - это ответ.