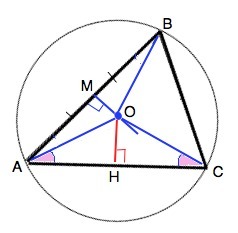
На серединном перпендикуляре стороны АВ треугольника АВС отмечена такая точка О , что угол ОАС = углу ОСА , Докажите что точка - центр окружности описанной около треугольника АВС

В ∆ АОС углы при основании АС равны.  Следовательно, ∆ АОС –равнобедренный, и АО=ОС. 

В ∆ АОВ отрезок ОМ⊥АВ и делит её пополам. ⇒

ОМ высота и медиана ∆ АОВ. ⇒ ∆ АОВ - равнобедренный, и 

АО=ОВ. Отрезки АО=ОВ=ОС 

Точки А, В и С находятся на одном и том же расстоянии от О, следовательно,  принадлежат окружности, так как ей принадлежит множество точек плоскости, находящихся на одном и том же расстоянии от одной точки, ⇒ 

т.О - центр описанной около ∆ АВС окружности, ч.т.д.