-
Найдите неизвестные стороны прямоугольного треугольника АВС(угол С=90°)если:
1)АС=8; tgB=3
2)AC=6; cosB=1/3
Ответы 1
-
Ответ:
1) BC=\dfrac{8}{3}
AB=\frac{8\sqrt{10}}{3}
2) BC=\dfrac{9\sqrt{2}}{2}
AB=\dfrac{27\sqrt{2}}{2}
Объяснение:
1) АС = 8, tg∠B = 3
Тангенс острого угла прямоугольного треугольника - это отношение противолежащего катета к прилежащему:
tgB=\dfrac{AC}{BC}
\dfrac{AC}{BC}=\dfrac{3}{1}
BC=\dfrac{AC}{3}
BC=\dfrac{8}{3}
По теореме Пифагора:
AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{8^{2}+(\frac{8}{3})^{2}}=
=\sqrt{64+\frac{64}{9}}=\sqrt{\frac{640}{9}}=\frac{8\sqrt{10}}{3}
2) AC = 6, cosB=\frac{1}{3}
Косинус острого угла прямоугольного треугольника - это отношение прилежащего катета к гипотенузе:
cosB=\dfrac{BC}{AB}=\dfrac{1}{3}
Пусть ВС = х, тогда АВ = 3х.
По теореме Пифагора составим уравнение:
AB² = AC² + BC²
(3x)² = 6² + x²
9x² = 36 + x²
8x² = 36
x^{2}=\dfrac{36}{8}=\dfrac{18}{4}
x=\dfrac{9\sqrt{2}}{2} x=-\dfrac{9\sqrt{2}}{2} - не подходит
BC=\dfrac{9\sqrt{2}}{2}
AB=3BC=\dfrac{27\sqrt{2}}{2}
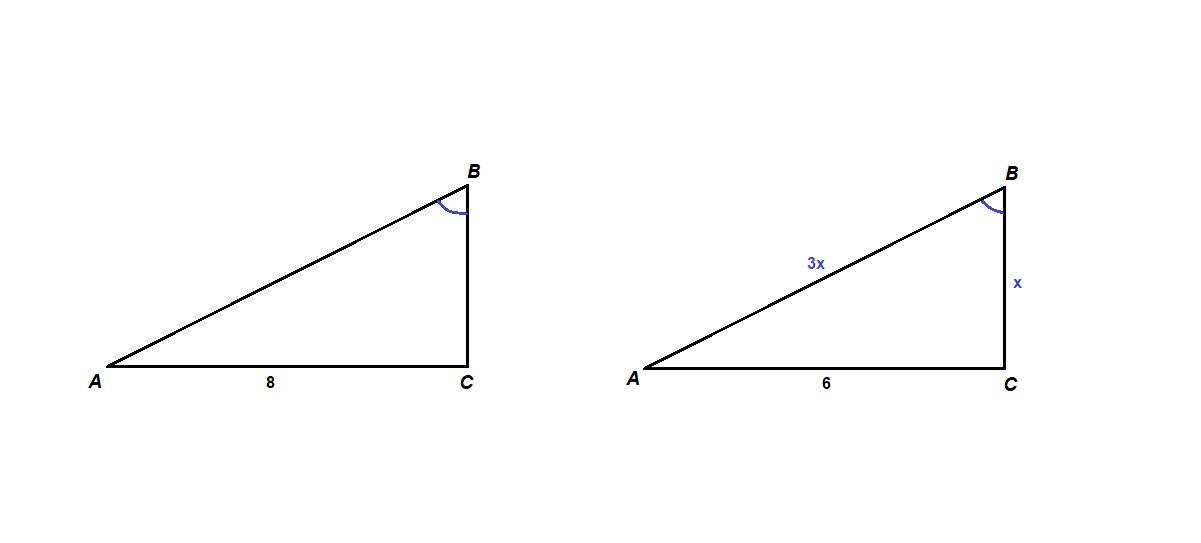
-
Автор:
amosv4ff - 2 года назад
-
5
-
-
Добавить свой ответ
-
1.If was able to/had been able to find an internet cafe, I would have sent you an email.
2.If you hadnt downloaded that program,your computer wouldnt have got/wouldnt get a virus.
3.If you didnt call/hadnt called me up,I wouldnt have sent you the file by email.
4.If I had bought a faster computer,I would have found/would find it easier to run this program.
5.If you had asked me,I would tell/would have told you what to do.
вы можете мне помочь
какой из них правильный-
Предмет:
Английский язык -
Автор:
captainuqvr - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
Характеристика Афони из рассказа Платонова цветок на земле 6 класс.
-
Предмет:
Литература -
Автор:
fabiolastephens - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Напишите о спортивной игре футбол
-
Предмет:
Обществознание -
Автор:
angel27 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
комедия ошибок шекспир! анализ, краткое содержание , всё)))) даю 50 б! срочно
-
Предмет:
Литература -
Автор:
kellyvwkt - 5 лет назад
-
Ответов:
1 -
Смотреть
-
