-
Дан треугольник MKP. Окружность с центром в точке О касается стороны PK в точке К и пересекает сторону MP в точке S. KM=18, KS=9, SP=7. Найти MS.
MK не является диаметром.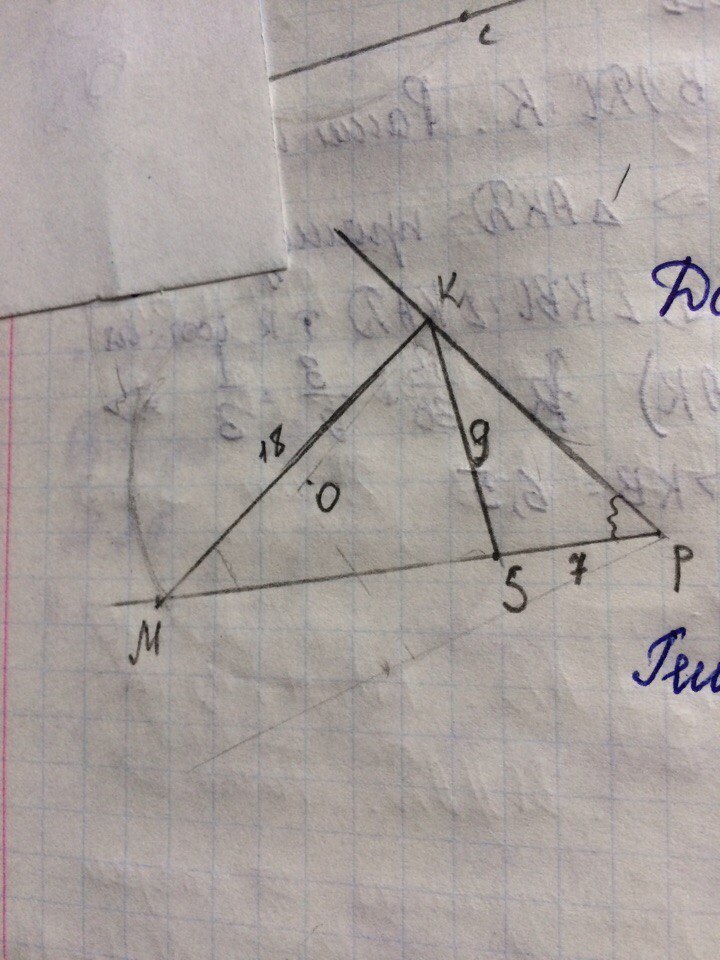
-
Предмет:
Геометрия -
Автор:
averybaker - 5 лет назад
-
Ответы 2
-
Спасибо большое
-
Автор:
sablestanton - 5 лет назад
-
0
-
-
Для данной окружности КР - касательная и МР - секущая.По теореме о касательной и секущей КР²=PS·MP, отсюда КР/PS=МР/КР. С таким отношением сторон и общим углом Р треугольники KSP и МКР подобны. Для них можно записать следующую пропорцию:PS/KS=КР/МК ⇒ КР=PS·MK/KS=7·18/9=14.Также КР/PS=МР/КР ⇒ МР=КР²/PS=14²/7=28.Итак, МS=MP-PS=28-7=21 - это ответ.
-
Автор:
evangelineschroeder - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогите пожалуйста! Буду благодарна!
1) Задача: Моторная лодка собственная скорость которой 12 км/ч,идет против течения реки.Скорость течения реки 1целая 1/5 км/ч.Какое расстояние пройдет моторная лодка за 3ч?
2) Задача: Для ремонта детского сада привезли 45 кг краски. Израсходовали 5/9 всей караски. Сколько килограммов краски израсходовали?
3) Задача: Для спортивных тренажеров выделены 3/7 всей площади спортивного зала,то есть 42м в квадрате.Чему равна площадь спортзала?
4) Задача: Вычисли периметр прямоугольника со сторонами 2 целых 1/4 м и 1 целая 1/2 м.
-
Предмет:
Математика -
Автор:
ming - 5 лет назад
-
Ответов:
2 -
Смотреть
-
- Какой лист у ежевики?
- 4*8 в степени x -7*12 в степени x+3*16 в степени x = 0
-
порівняйте новгородську республіку та московську державу
-
Предмет:
История -
Автор:
bessieb9kj - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
