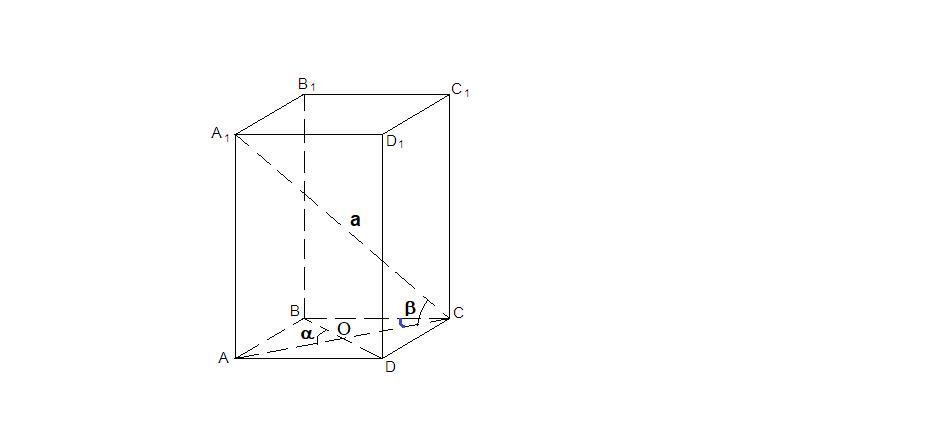
У прямокутному паралелепіпеді діагональ дорівнює а і нахилена до площини основи під кутом B(бета). Кут між діагоналями основи дорівнює а. Знайдіть бічну поверхню паралелепіпеда.

Ответ:  

    Sбок = a²sin2β (sin(α/2) + cos(α/2))

Объяснение:

Все грани прямоугольного параллелепипеда - прямоугольники.

ΔА₁АС:   ∠A₁AC = 90°

              sinβ = AA₁ / A₁C,   ⇒   AA₁ = A₁C · sinβ,

              AA₁ = a · sinβ

              cosβ = AC / A₁C,   ⇒  AC = A₁C · cosβ,

              AC = a · cosβ.

Точка пересечения диагоналей прямоугольника является центром описанной окружности. Тогда для окружности, описанной около прямоугольника ABCD ∠АОВ - центральный, а ∠ACB - вписанный, опирающийся на ту же дугу, значит

∠АCB = 1/2 ∠AOB = α/2.

ΔABC:   ∠ABC = 90°

             sin∠ACB = AB / AC,  ⇒  AB = AC · sin∠ACB,

             AB = a · cosβ · sin(α/2),

             cos∠ACB = BC / AC,  ⇒  BC = AC · cos∠ACB,

             BC = a · cosβ · cos(α/2).

Sбок = Pосн · AA₁

Sбок = (AB + BC) · 2 · AA₁

Sбок = (a · cosβ · sin(α/2) + a · cosβ · cos(α/2)) · 2 · a · sinβ =

= a · cosβ(sin(α/2) + cos(α/2)) · 2 · a · sinβ =

= 2a²sinβ·cosβ(sin(α/2) + cos(α/2)) =

= a²sin2β (sin(α/2) + cos(α/2))