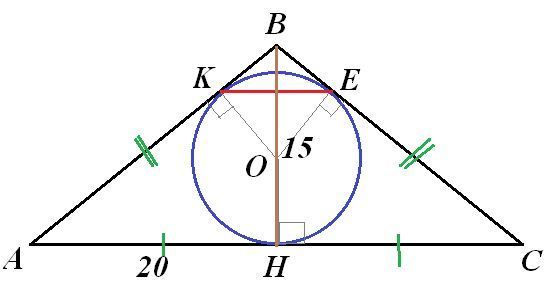
Основа рівнобедреного трикутника дорівнює 40 см, а висота, проведена до неї, - 15 см. Знайдіть відстань між точками дотику кола, вписаного у трикутник, з його бічними сторонами.

Пусть в равнобедренный ΔАВС с основанием АС=40см, ВН=15см - высота. Вписанная окружность касается сторон треугольника в точках К, Е и Н.По свойству равнобедренного треугольника АН=НС=20см. АВ=ВС.По свойству отрезков касательных, проведенных к окружности из одной точки  АН=АК=20см=НС=СЕ, а также ВК=ВЕ.Из прямоугольного ΔАВН по теореме Пифагора АВ²=АН²+ВН² = 20²+15²=625, т.е. АВ=25см. Тогда ВК=ВЕ=АВ-АК=25-20=5(см).Рассмотрим ΔАВС и ΔВКЕ. Они подобны по II признаку (Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны). У них ∠КВЕ=∠АВС, а стороны их образующие  \frac{BK}{BA} = \frac{BE}{BC} = \frac{5}{25} Из подобия следует отношение  \frac{5}{25} = \frac{KE}{AC} \frac{1}{5} = \frac{KE}{40} ,\ KE=8Ответ: КЕ=8см.