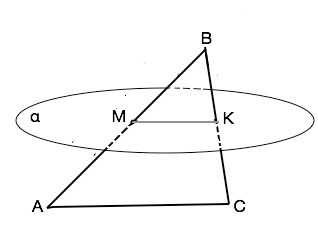
Дан треугольник АВС. Точка М принадлежит АВ, точка К принадлежит ВС.
ВМ:МА=3:4. Через МК проходит плоскость альфа, параллельная АС.
Доказать, что ВС:ВК=7:3 и найти длину МК, если АС=14 см

Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей. (свойство)

Плоскость α параллельна АС, следовательно, МК, линия пересечения плоскостей АВС и α,  параллельна АС.

В ∆ АВС МК║АС. Поэтому соответственные ∠ВМК и ∠ВАС равны, угол В общий для треугольников АВС и МВК, ⇒ эти треугольники подобны.

Примем коэффициент подобия равным а. 

ВК:СК=ВМ:МА=3а:4а, ⇒ВС=ВК+СК=7а.

k=ВС:ВК=7:3 - (доказано). 

Отсюда АС:МК=7:3

14:МК=7:3 ⇒ 7МК=42,

МК=6 см