Объём треугольной пирамиды равен 35. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 3:4, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.

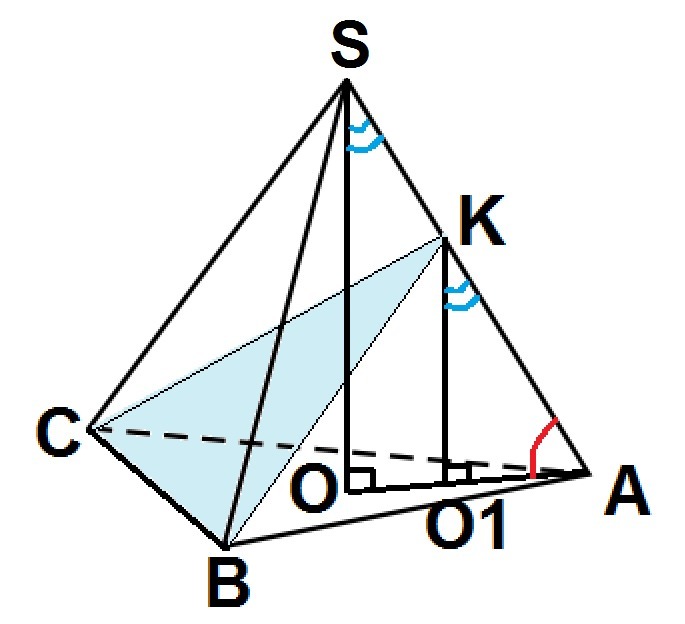
Пусть SABC - треугольная пирамида. Плоскость проходит через сторону BC основания этой пирамиды и пересекает противоположное боковое ребро AS в точке K так, что SK : AK = 3 : 4.Треугольник BCK - сечение пирамиды SABC плоскостью, которая разбивает пирамиду SABC на две пирамиды - SKBC и KABC. Объем пирамиды SABC:V₁ = 1/3 * Sосн₁ * h₁где Sосн₁ - площадь треугольника, лежащего в основании данной пирамиды, т.е. S(ABC)h₁ - высота пирамиды SABC, т.е. перпендикуляр SO, проведенный к плоскости основания данной пирамидыОбъем пирамиды KABC:V₂ = 1/3 * Sосн₂ * h₂где Sосн₂ - площадь треугольника, лежащего в основании данной пирамиды, т.е. S(ABC) ⇒ Sосн₁ = Sосн₂h₂ - высота пирамиды KABC, т.е. перпендикуляр KO₁, проведенный к плоскости основания данной пирамидыТреугольники SOA и KO₁A подобны по двум углам:∠KAO₁ = ∠SAO (угол наклона ребра к плоскости ABC)∠SOA = KO₁A = 90°⇒ стороны данных треугольников пропорциональны. Поскольку SK : AK = 3 : 4, отрезок SK составляет 3 части, отрезок AK составляет 4 части, AS составляет 7 частей.⇒ AK : AS = 4 : 7 ⇒ KO₁ : SO = 4 : 7 ⇒ h₂ : h₁ = 4 : 77h₂ = 4h₁h₂ = 4h₁ / 7  V₁             1/3 * Sосн₁ * h₁---------- = -----------------------------  V₂             1/3 * Sосн₂ * h₂  V₁              S(ABC) * h₁----------- = -----------------------  V₂              S(ABC) * h₂  V₁              h₁--------- = -----------  V₂              h₂  V₁               h₁---------- = -----------------  V₂              4h₁ / 7  35             7--------- = ---------  V₂             435 * 4 = 7V₂V₂ = 20 (куб. ед.) 20 составляет бОльшую часть от 35 ⇒ это и есть бОльший из объемов, на которые плоскость разбивает исходную пирамиду.