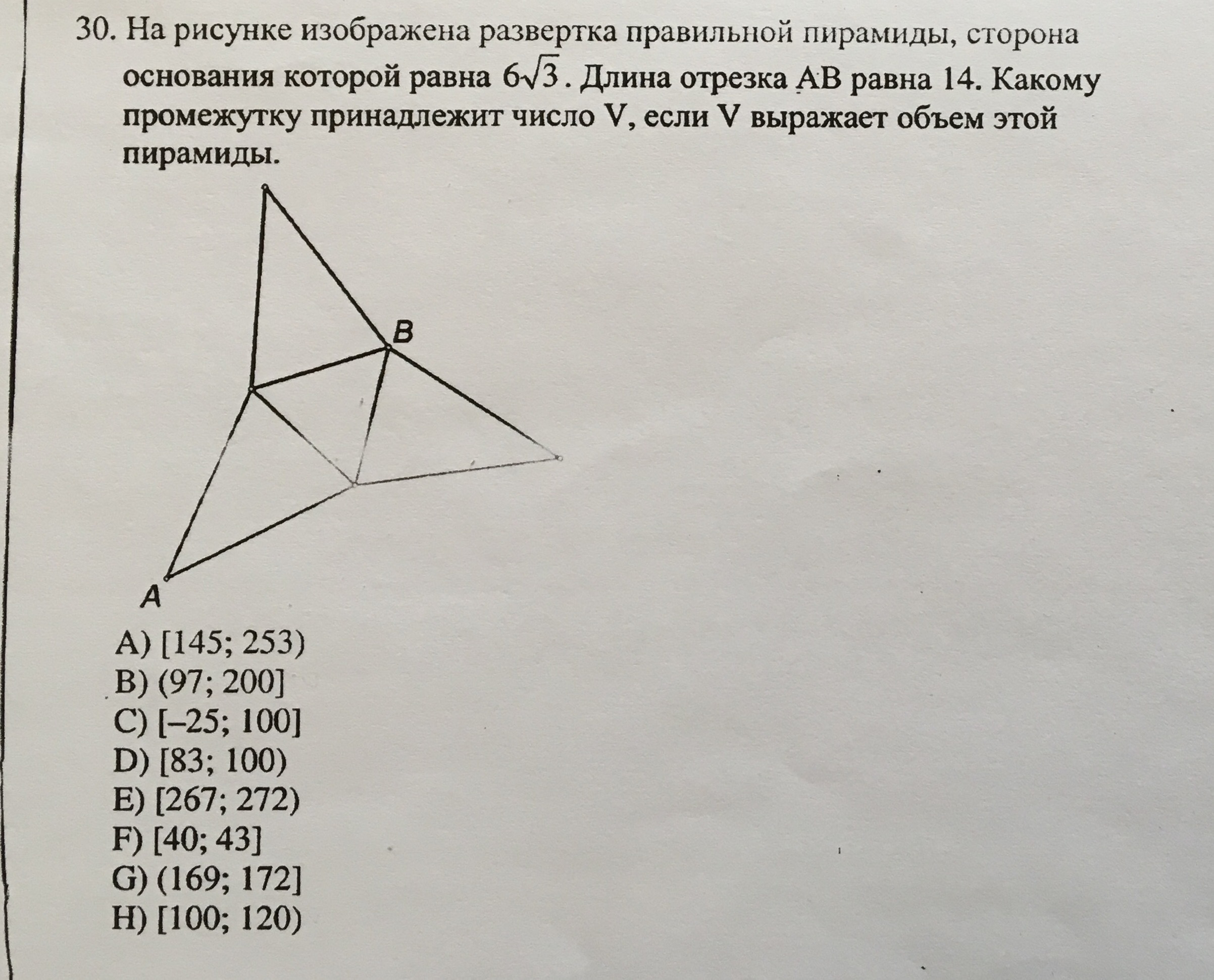
На рисунке изображена развертка правильной пирамиды, сторона основания которой равна 6√ 3. Длина отрезка AB равна 14. Какому промежутку принадлежит число V, если V выражает объем этой пирамиды.

Дано:   - сторона основания правильной треугольной пирамиды а = 6√3,  - длина отрезка AB равна 14.Отрезок АВ - это сумма высоты h основания и высоты A боковой грани (апофемы).Высота h основания (равностороннего треугольника) равна:h = a*cos 30° = 6√3*(√3/2) = 9.Апофема А = 14 - 9 = 5.Апофема представляет собой гипотенузу прямоугольного треугольника, один катет которого - высота Н пирамиды, второй - (1/3) высоты основания h (она же и медиана).Находим высоту пирамиды:Н = √(А²-(h/3)²) = √(25-9) = √16 = 4.Площадь основания So = a²√3/4 = 108*√3/4 = 27√3.Объём V пирамиды равен: V = (1/3)SoH = (1/3)*27√3*4 = 36√3 ≈  62,3538 куб. ед.Ответ: промежуток С) = [-25; 100].