-
помогите,пожалуйста, только без синусов и косинусов и плиз подробно, спасибо большое заранее
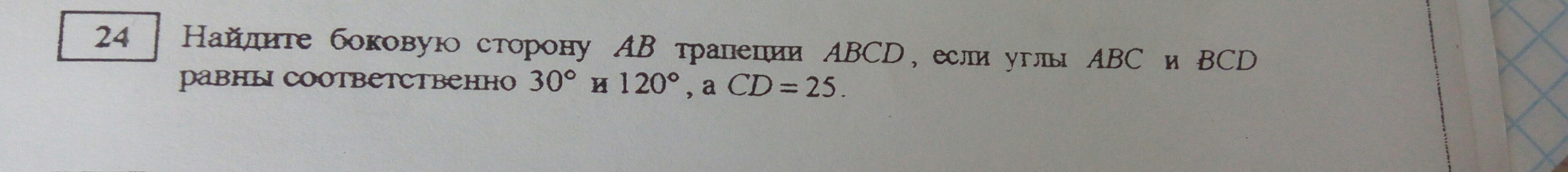
Ответы 1
-
Сумма углов, прилежащих к боковой стороне трапеции равна 180°.∠ADC = 180° - ∠BCD = 180° - 120° = 60°Проведем две высоты АК и СН.ΔDCH: ∠DHC = 90°, ∠HDC = 60°, ⇒ ∠HCD = 30°. HD = CD/2 = 25/2 как катет, лежащий напротив угла в 30°. По теореме Пифагора CH = √(CD² - HD²) = √(625 - 625/4) = √(3·625/4) = 25√3/2AK = CH = 25√3/2ΔABK: ∠AKB = 90°, ∠ABK = 30°, ⇒ AB = 2AK = 2 · 25√3/2 = 25√3 по свойству катета, лежащего напротив угла в 30°

-
Автор:
terminator3yrw - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
СРОЧНО!!!!!
три числа образуют возрастающую арифметическую прогрессию а их квадраты составляют геометрическую прогрессию найдите эти числа если их сумма равна 42
2) первая труба наполняет резервуар на 6 минут дольше чем вторая обе трубы наполняют этот же резервуар за 4 минут за сколько минут наполняет этот резервуар первая и вторая труба
3) [tex] \sqrt[3]{11+4x}+ \sqrt[3]{15-4x}=13 [/tex]-
Предмет:
Алгебра -
Автор:
biscuitwhsz - 5 лет назад
-
Ответов:
3 -
Смотреть
-
- найти значение k и b и построить график функций вида y=kx+b через точку a(-3 1) И параллельный графику функций y=2x
-
Решите пожалуйста по действия!!Ответ должен быть,,12,,
-
Предмет:
Математика -
Автор:
boywashington - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Дано:
Сумма 1200 руб
Цена: 1 л. молока - 100 руб
Объем 1 банки - 3 литра
Сколько банок молока можно купить на 1200 руб?
И пишите пожалуйста, что вы нашли, после каждого действия
-
Предмет:
Математика -
Автор:
willieizd3 - 5 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
