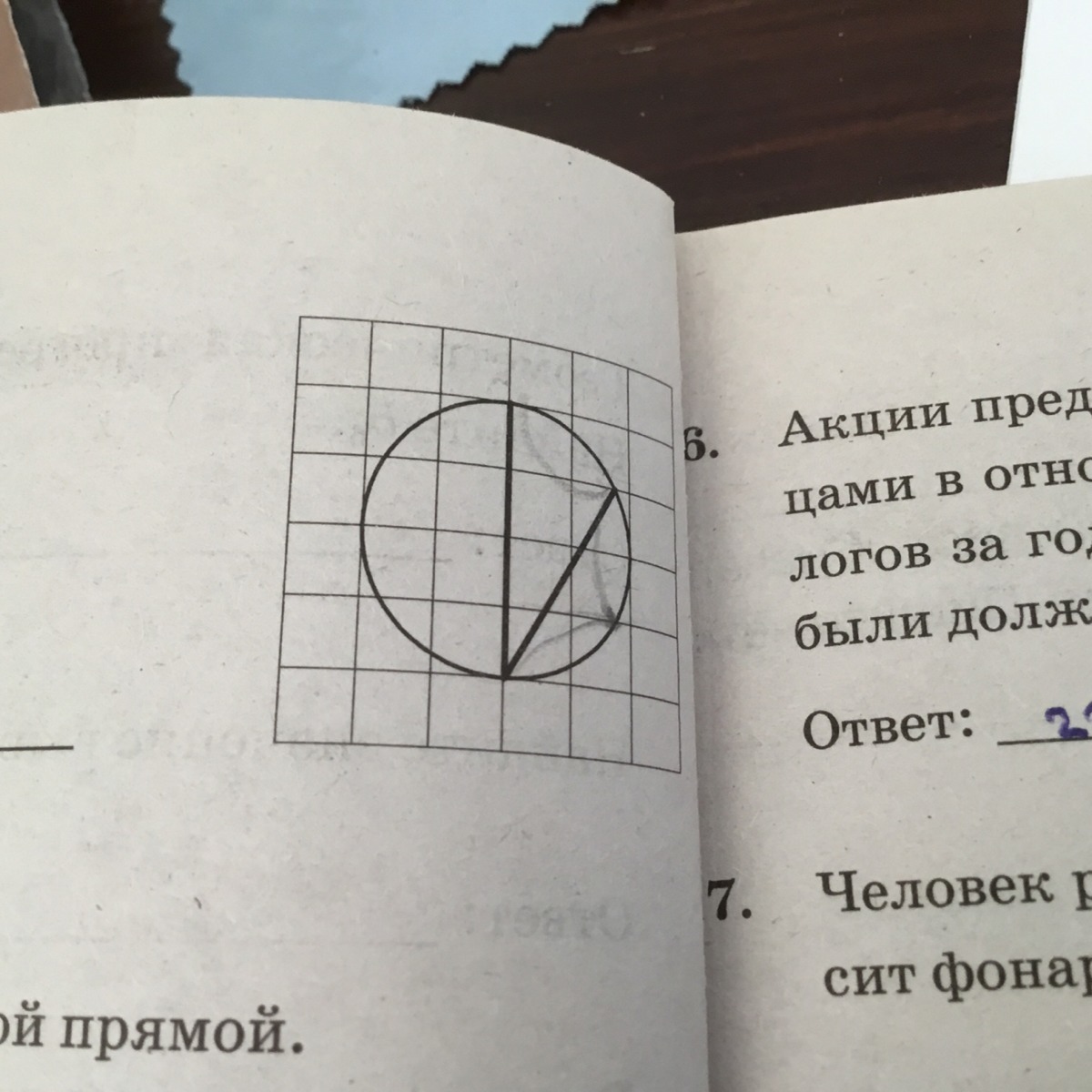
На клетчатой бумаге изображен угол найдите его градусную величину

К сожалению, ответить на этот вопрос, опираясь на картинку во вложении, весьма затруднительно. Рискну предположить, что взяв циркуль и измерив им длину меньшей хорды увидим, что она равна половине диаметра (гипотенузы прямоугольного треугольника). По свойству - против угла 30° лежит катет в два раза меньше гипотенузы. И наоборот. Следовательно искомый угол 30°.

AC=4; AH=1∠ABC - прямой, т.к. опирается на диаметр. Треугольник ABC - прямоугольный. Высота, проведенная из вершины прямого угла, делит гипотенузу на отрезки: AH= AB^2/AC; CH= BC^2/ACAH=AB^2/AC <=> AB^2=AH*AC <=> AB=√4=2Катет против угла 30° равен половине гипотенузы. Верно и обратное: если катет равен половине гипотенузы, то он лежит против угла 30°.AB=AC/2 => ∠ACB=30°