100 баллов + лучший ответ! Апофема правильной четырёхугольной пирамиды равна 2 корень из 3 и наклонена к плоскости основания на 60 градусов. Найти объём пирамиды.

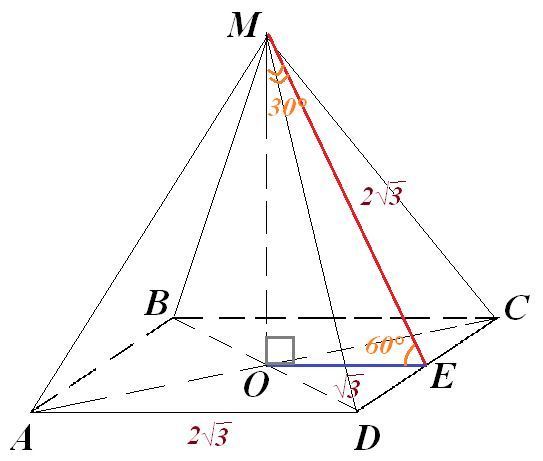
Пусть MABCD - данная правильная пирамида, ее апофема - МЕ.

Проведем высоту МО.

V= \frac{1}{3}S_{OCH}*H= \frac{1}{3}S_{ABCD}*MO

В прямоугольном Δ МЕО ∠ ОМЕ = 90°-60° = 30°.

Значит, катет ОЕ равен половине гипотенузы МЕ: ОЕ=√3.

Т.к. пирамида правильная, то Е - середина DC.

Точка О - середина АС. Значит, ОЕ - средняя линия ΔACD. Тогда ОЕ||AD и AD=2OE =2√3

Значит, S_{OCH}=S_{ABCD}=(2 \sqrt{3})^2=12

В прямоугольном Δ МЕО по тереме Пифагора МО² = МЕ² - ОЕ²

MO= \sqrt{12-3} =3

Таким образом, V= \frac{1}{3}*12*3=12

Ответ: 12.