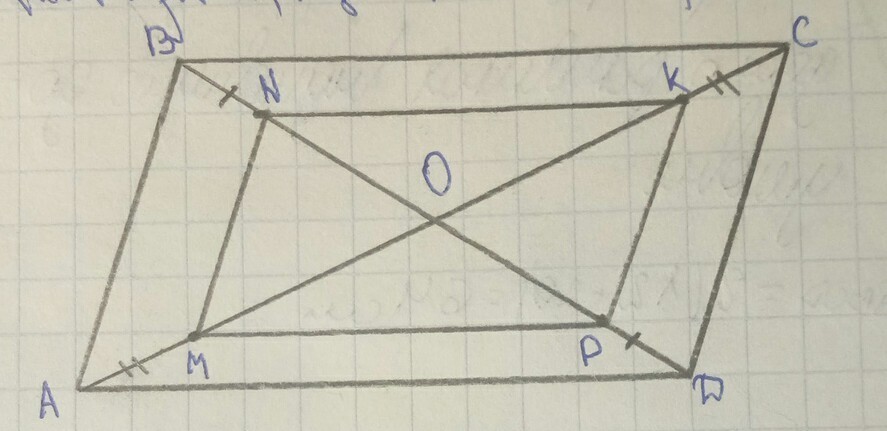
На рисунке ABCD параллелограмм, AM=KC, BN=PD. Докажите, что MP=NK, MN||PK

ABCD параллелограмм, AM=KC, BN=PD

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. 

МО=АО -АМ, ОК=СО - КС. По условию АМ=СК, следовательно, МО=ОК. 

Аналогично доказывается равенство NO=ОР. 

МО=ОK, NO=OД. Диагонали четырехугольника МNKP пересекаются и точкой пересечения делятся пополам. Из признаков параллелограмма:

Если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам, то этот четырехугольник ― параллелограмм. ⇒ МNKP- параллелограмм.

В параллелограмма противоположные стороны равны и параллельны. Следовательно, MP=NK, MN||PK, что и требовалось доказать.