-
Задача 1.
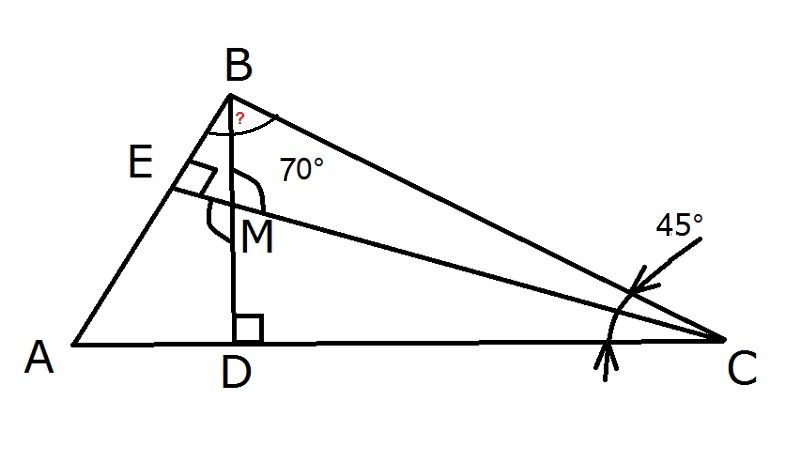
висоти BD і CE трикутника ABC перетинаються в точці М .Здайдіть кут ABC, якщо кут ACB=45°, кут BMC=70°
Задача 2.
У трикутнику ABC кут С=90°, кут А=30°, відрізок BM -бісектриса трикутника. Знайдіть довжину катета AC ,якщо ВМ=6 см.
Помогите пожалуйста решить геометрія
Ответы 1
-
Задача 1.∠BMC = ∠EMD = 70° (вертикальные углы).Рассмотрим четырехугольник AEMD:∠BAC = 360° - (∠AEM + ∠ADM +∠EMD) (сумма углов четырехугольника = 360°)т.к. BD и CE - высоты (по усл) , то ∠AEM = ∠MDA = 90°.Найдем ∠BAC:∠BAC = 360° - (90° + 90° + 70°) = 110°∠ABC = 180° - (∠ACB + ∠BAC) (сумма углов треугольника = 180°)∠ABC = 180° - (45° + 110°) = 25°.Ответ: 25°Задача 2.Т.к. BM - биссектриса, то ∠CBM=∠MBAРассмотрим ΔABC: ∠C=90° (по усл), ∠A=30° (по усл) ⇒ ∠B = 180° - (90°+30°)=60°⇒ ∠CBM=∠MBA=1/2∠B=30°Рассмотрим ΔAMB: ∠MAB = ∠ABM ⇒ треугольник равнобедренный ⇒ MA=MB=6 смРассмотрим ΔCMB: ∠C=90°, ∠MBC=30°. Вспоминаем, что катет, лежащий против угла 30° равен половине гипотенузы ⇒MC = 1/2 MB = 3 смAC = AM + MC = 6 см + 3 см = 9 см
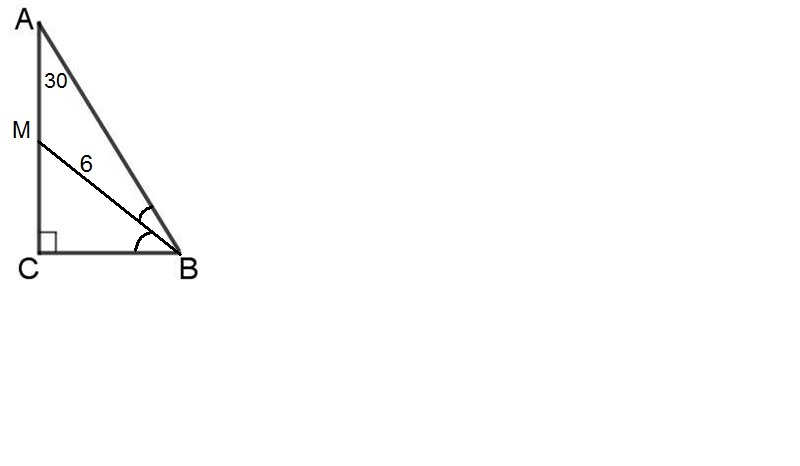
-
Автор:
josuéschultz - 2 года назад
-
14
-
-
Добавить свой ответ
Еще вопросы
-
после того как портниха истратила 8 катушек ниток,у неё осталось по 4 катушки белых, черных, и цветных ниток.солько катушек ниток было у неё в начале?
-
Предмет:
Математика -
Автор:
cookie doughvzet - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
скласти речення зі словами тачскрин мануал смартфон
-
Предмет:
Русский язык -
Автор:
george39 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
ОТВЕТИТЬ НА ВОПРОСЫ
Американские индейцы никогда не подчинялись никаким законам, никакой власти или тени какого-либо правительства. Их единственный руководитель -- это обычай и то нравственное сознание добра и зла, которое, как чувство вкуса и осязания, в каждом человеке составляет часть его природы. Поступки, нарушающие то, что считается между ними должным, наказываются презрением и исключением из общества; в случаях же более важных, как грабеж, убийство, наказание предоставляется тем лицам, которые пострадали. Как ни кажутся несовершенны эти способы наказаний, преступления очень редки между ними.
1) чему подчинялись американские индейцы? Какие наказания у них существовали?
2) каким этапам развития общества свойственно регулирование всей жизни людей посредством обычаев? Обоснуйте свой ответ.-
Предмет:
Обществознание -
Автор:
allysonyd8y - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Что означает понятие малая Родина?
-
Предмет:
Другие предметы -
Автор:
nathan68 - 5 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
