Дам 45 баллов

Через середину O диагонали MK параллелограмма mnkp проведена прямая, пересекающая стороны NK и MP соответственно в точках A и B.
Докажите, что MAKB параллелограмм.

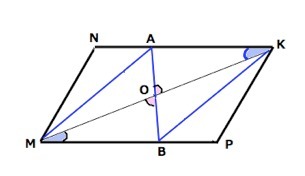
Обозначим середину диагонали MK точкой О. 

Рассмотрим ∆ АОК и ∆ МОВ. 

Их углы при вершине О равны как вертикальные, а ∠АКО=∠ВМО как накрестлежащие. МО=ОК по условию 

∆ АОК=∆ МОВ  по второму признаку равенства треугольников. 

Т.к. АК и МВ лежат на сторонах параллелограмма, они параллельны, а из равенства треугольников и равны. 

Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.

⇒ МАКВ - параллелограмм.