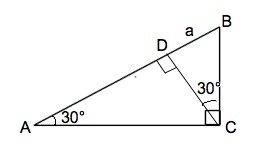
в треугольнике abc с углами acb= 90, bac= 30 проведена, высота cd. Найдите сумму длин катетов треугольника abc, если BD + CD= 2017

Высота, проведенная к гипотенузе, делит прямоугольный треугольник на подобные треугольники. 

∆ АВС~∆ BCD,⇒ угол ВСD=30°.

В ∆ BCD катет DB  противолежит углу 30°, значит, гипотенуза СВ=2•BD.

Аналогично в ∆ АСD гипотенуза АС=2•CD⇒

АС+ВС=2•(BD+CD)

AC+BC=2•2017=4034

–––––––––

Или, если нужны вычисления:

Примем ВD=a 

Тогда CD=BD:ctg30=a√3

CD+BD=а(1+√3)

ВС=BD:sin30°=2а, 

АС=ВС:ctg30=2a√3

 АС+ВС=2а(1+√3) - вдвое больше  BD+CD ⇒

АС+ВС=1017•2=4034