-
Дано:треугольник KHM и треугольник ОMB
KM=MB ,HM=MD
Доказать :треугольник KHM=DMB
Помогите пожалуйста ❤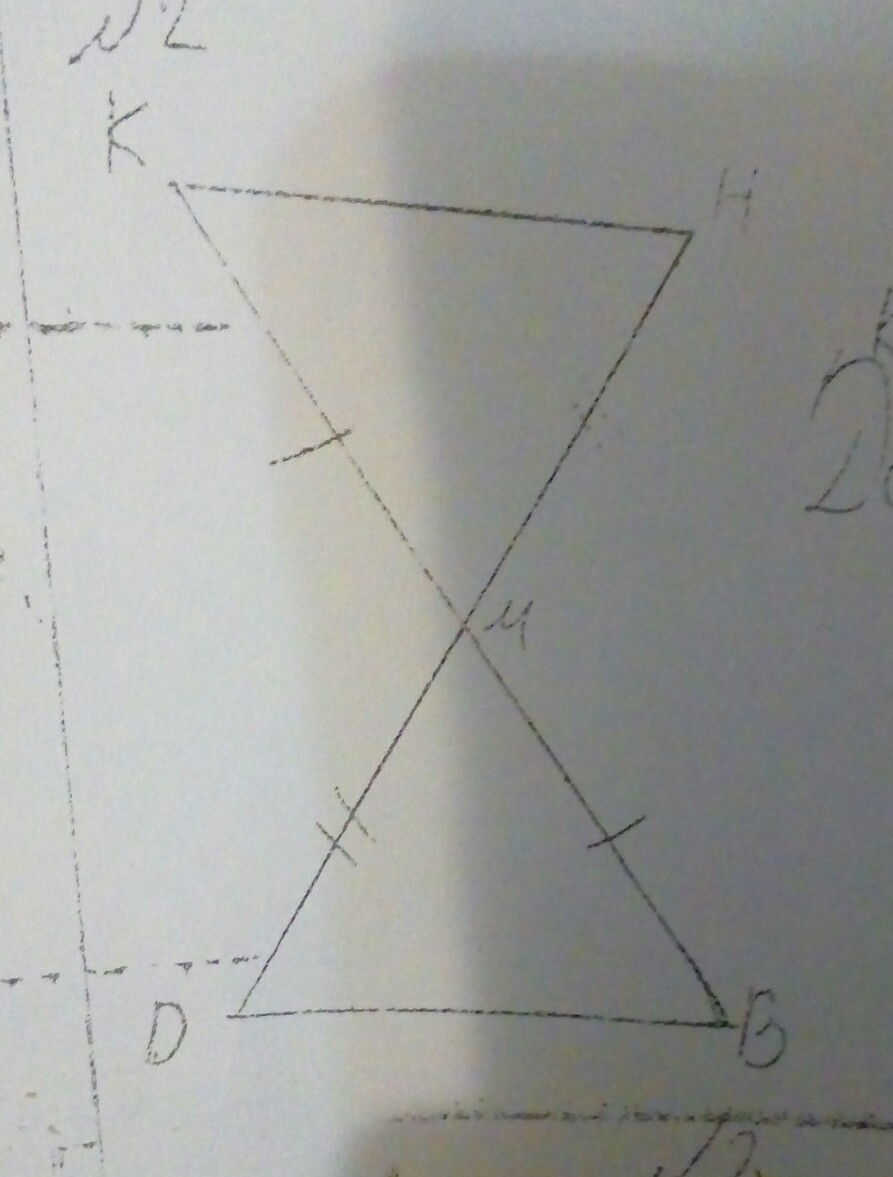
Ответы 2
-
дано: треугольник KMN, AK=BN, AM=BM, CA перпендикулярно KM, CB перпендикулярно NMдоказать: MC - медиана треугольника KMNВ треугольнике KMN боковые стороны состоят из равных отрезковAK=BN, AM=BM, следовательно
КМ=МК+АМ=ВN+MB=MN
Треугольник KMN - равнобедренный.
Δ КАС=Δ СВN,
так как это прямоугольные треугольники,
углы К и N равны как углы при основании равнобедренного треугольника,
катеты КА=ВN. Если в прямоугольном треугольнике острый угол и катет равен острому углу и катету другого прямоугольного треугольника, то эти треугольники равны.
Следовательно, гипотенузы АС и CN этих треугольников равны.АС=СN Точка С - середина стороны КNМС - медиана треугольника KMN, что и требовалось доказать.
-
Автор:
rafaelbishop - 5 лет назад
-
0
-
-
Доказательство: по двум сторонам и углу между нимиПо условии уже сказано, что КМ=МВ, НМ=МD и углы КМН и DМВ равны как вертикальные углы
-
Автор:
braveheart37 - 5 лет назад
-
0
-
-
Добавить свой ответ
-
ребят помагите пж
это причастный оборот:
слышавший шорох
управляемая по радио модель
подгоняемая ветром лодка.
составьте придложение с определяемым словом
пж помагите
-
Предмет:
Русский язык -
Автор:
kidoz88 - 5 лет назад
-
Ответов:
5 -
Смотреть
-
-
Объясните каково назначение предметного столика.
-
Предмет:
Биология -
Автор:
mitzizamora - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Что будет на англиском ,,ПРОШЛИ, ,
-
Предмет:
Английский язык -
Автор:
kcda1z - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите решить
3(4x+13)-25=74
-
Предмет:
Математика -
Автор:
justicebskb - 5 лет назад
-
Ответов:
2 -
Смотреть
-
