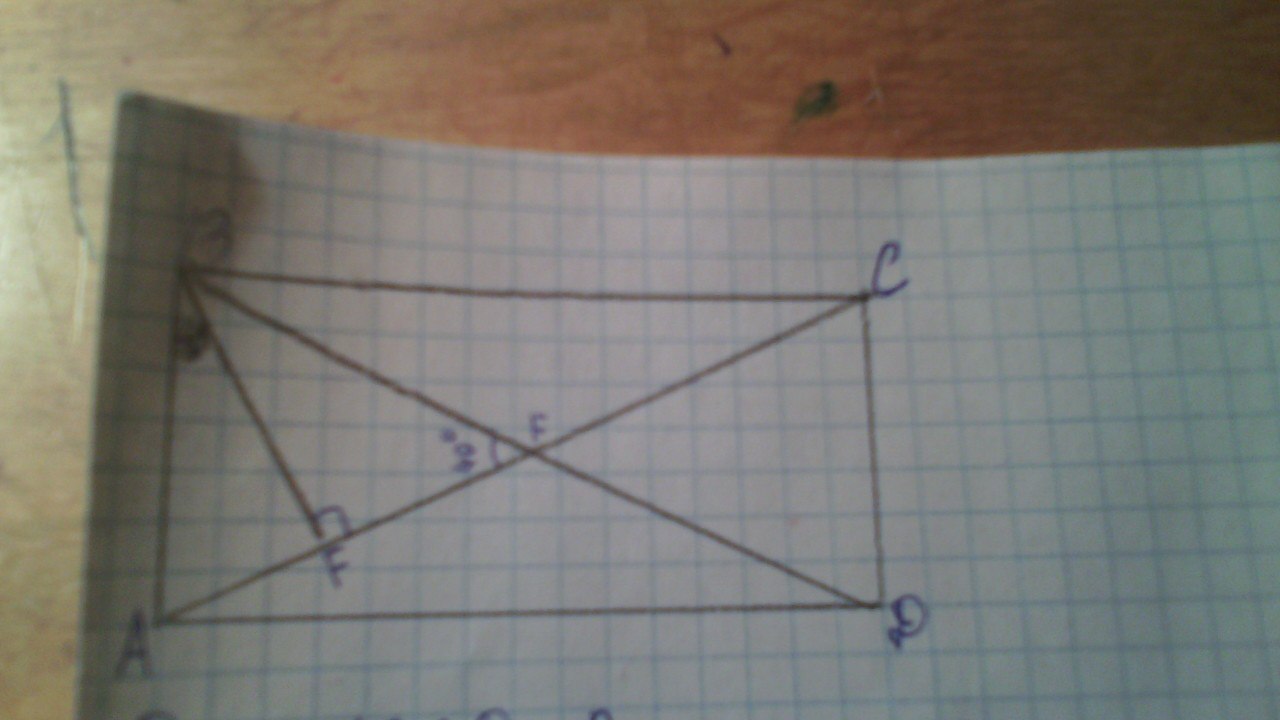
Дано:ABCD- прямоугольник; BF-перпендикуляр угол F=40 градусов
Найти: угол ABF
Геометрия 8 класс

Дано: ABCD - прямоугольник; AC∩BD=O; F∈AO; BF⊥AO; ∠AOB=40°.

Найти: ∠ABF.

Решение: ∠FOB = ∠AOB = 40° - как углы с одинаковыми сторонами.

ΔBFO - прямоугольный т.к. BF ⊥ AO. Значит ∠FBO = 90° - ∠FOB (т.к. сумма острых углов в прямоугольном треугольнике равна 90°). ∠FBO = 90° - 40° = 50°.

∠BOC и ∠AOB смежные, поэтому ∠COB  = 180° - ∠AOB = 180° - 40° = 140°.

Диагонали в прямоугольнике равны и делятся точкой пересечения пополам, поэтому ΔBOC - равнобедренный (BC - основание). Из этого следует, что ∠OBC = (180°-∠BOC)÷2 = 40°÷2 = 20°

∠ABC = 90° - как угол прямоугольника, поэтому

∠ABF = 90° - ∠FBO - ∠OBC = 90° - 50° - 20° = 20°.

Ответ: ∠ABF = 20°.

Вариант решения.

Ответ: 20°

Объяснение:

Диагонали прямоугольника равны и точкой пересечения делятся пополам.  Пусть диагонали пересекаются в точке О.

OB=OA, ∆ ВОА - равнобедренный.

Из суммы углов треугольника ∠ОВА=∠ОАВ=(180°-40°):2=70°

Т.к. BF⊥AC ( дано и см. рисунок вопроса), треугольник ВОF прямоугольный. Сумма острых углов прямоугольного треугольника 90° ⇒ ∠OBF=90°-40°=50°.

Угол АВF=∠ABO-∠OBF=70°-50°=20°